Дано:
Прямой круговой конус с углом при вершине катится по неподвижной плоскости без скольжения делая n оборотов в минуту около вертикальной оси
. Высота конуса — h.
Определить:
1. Алгебраические величины проекций угловых скоростей прецессии и ротации на оси и
, соответственно, а также мгновенную угловую скорость конуса.
2. Угловое ускорение конуса.
3. Скорости точек B и C.
4. Ускорение точки B, а также осестремительное и вращательное, нормальное и касательное ускорения точки C.
h = 20cm; n = 120 об./мин.
Решение:
1. Точка O — неподвижная точка конуса — начало отсчёта главной и подчинённой
координатных систем;
— ось прецессии,
— ось ротации.
2. Определить угловые скорости прецессии и ротации
, мгновенную угловую скорость
и мгновенную ось вращение
.
, так как
— константа
— угловая скорость нутации,
— угол нутации, тогда
определить угловую скорость прецессии по заданному числу оборотов .
оси
оси
векторное равенство на рисунке.
применим теорему синусов
тогда:
Проверим, выполняются ли условия регулярной прецессии:
3. В случае регулярной прецессии угловое ускорение конуса является закреплённым вектором в точке O и определяется по формуле:
Комментарий: По правилу векторного произведения (см.рис) вектор .
4. Определить скорости точек B и C конуса по формуле
Комментарий: По правилу векторного произведения (см.рис.)
тогда
4.1 Так как точка C оси ротации
, то ускорение точки C можно определить по формуле:
где
— нормальное и касательное ускорения точки C, соответственно.
так как
так как , тогда
;
Комментарий: , так как
(см.рис.)
4.2 Определить осестремительное ускорение точки C.
Вращательно ускорение точки C:
Комментарий:
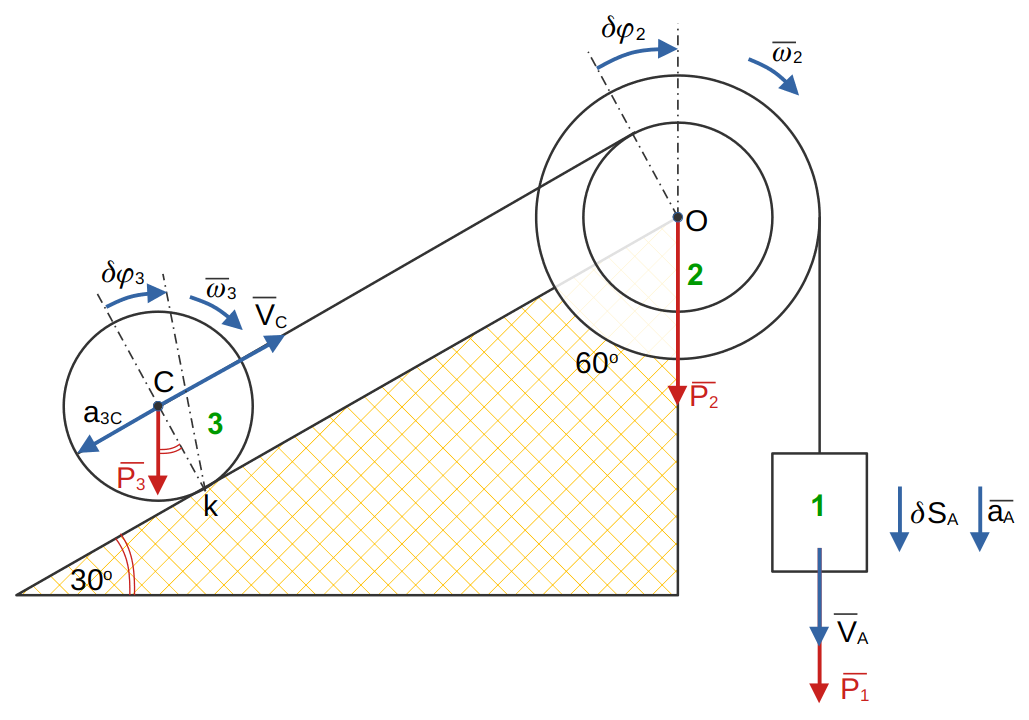
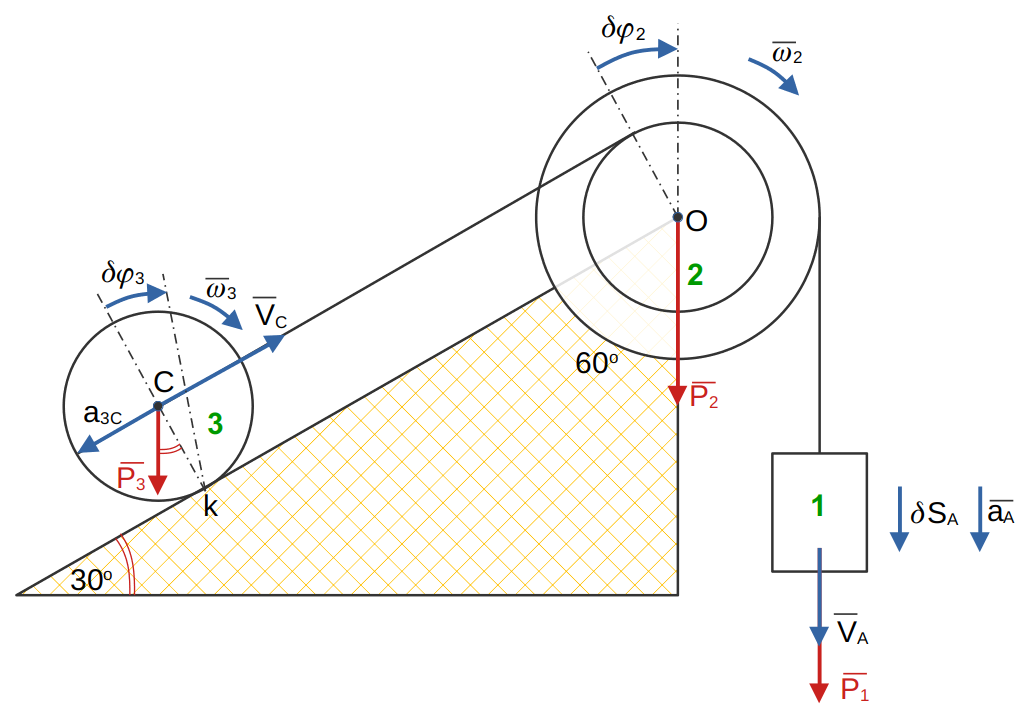
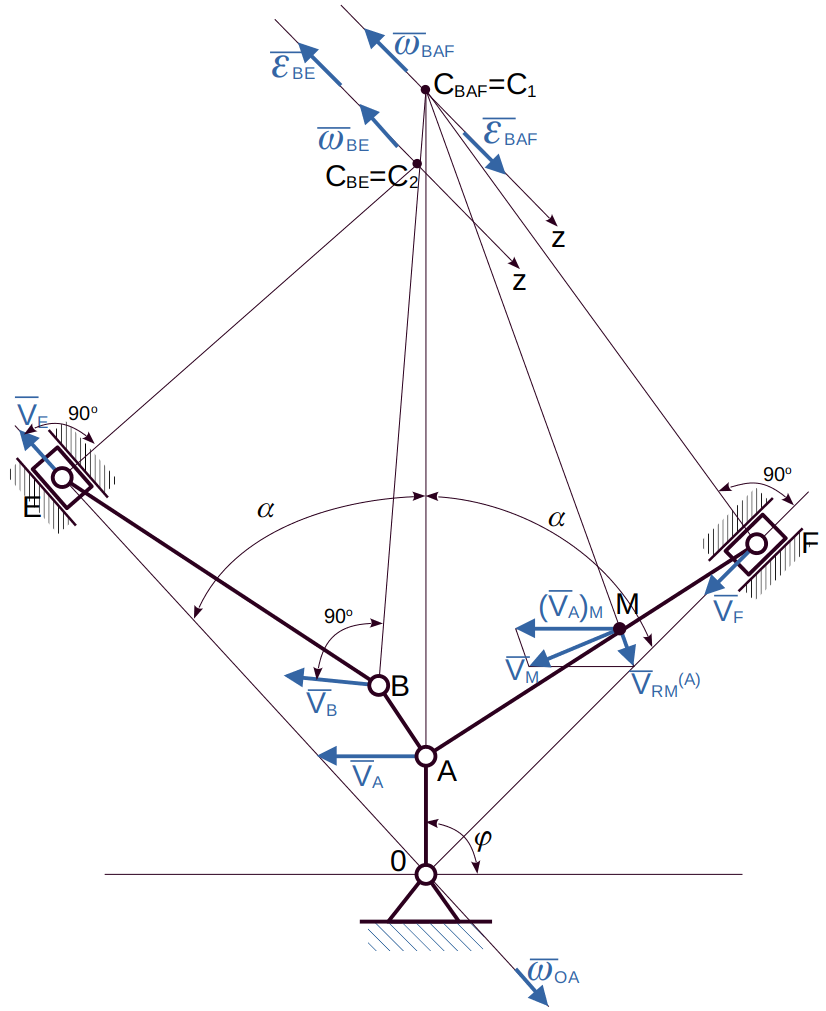
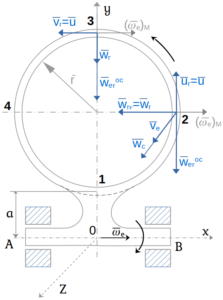 Полое кольцо радиуса r жестко соединено с валом АВ, и притом так, что ось вала расположена в плоскости оси кольца. Кольцо заполнено жидкостью, движущейся в нем в направлении стрелки часов с постоянной относительной скоростью U.
Полое кольцо радиуса r жестко соединено с валом АВ, и притом так, что ось вала расположена в плоскости оси кольца. Кольцо заполнено жидкостью, движущейся в нем в направлении стрелки часов с постоянной относительной скоростью U.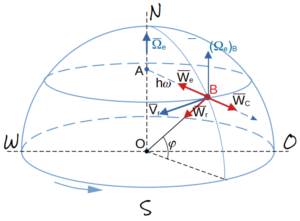
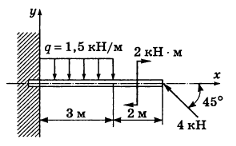 Дано:
Дано: Дано:
Дано: