Тело брошено под углом к горизонту со скоростью
. Определить уравнение траектории тела. Силами сопротивления пренебречь. Оси
и
изображены на рисунке.
Дано: 
Определить: 
каноническое уравнение траектории
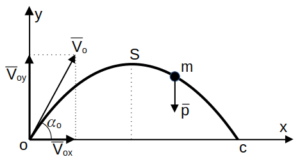 Начальные условия:
Начальные условия:
,
Запишем векторное уравнение динамики материальной точки.
(1)
(2)
(3)
Проинтегрируем уравнения (2) и (3) по отдельности с помощью неопределённых интегралов:
Для уравнения (2):
(произвольная постоянная находится из начальных условий)
(произвольная постоянная находится из начальных условий)
Подставляя найденные постоянные и
, получим уравнение
(4)
Для уравнения (3):
(произвольная постоянная находится из начальных условий)
(произвольная постоянная находится из начальных условий)
Подставляя найденные постоянные и
, получим уравнение
(5)
Уравнения (4) и (5) — уравнения траектории точки в параметрическом виде;
теперь определим канонический вид уравнения траектории точки.
Из уравнения (4) получим
(6)
Подставляя (6) в уравнение (5) получим
(7)
Получили канонический вид уравнения траектории точки: — парабола!
Примечание:
Вид уравнения (7) зависит только от угла бросания и начальной скорости
.
Из этого уравнения видно, что траектория не зависит от массы точки.
Это является результатом, используемым в «Основной задаче внешней баллистики» («Параболической теории»).
Таким образом, не зависимо от калибра снаряда его траектория всегда будет параболической, но при условии отсутствия сопротивлению движению.
«Параболическая теория» справедлива для описания движения снарядов больших калибров, летящих с малой скоростью.