26.1 [Мещерский И.В. Задачи по теоретической механике. // Изд-во. «Лань», 2008]

В шахте равноускоренно опускается лифт массой m=280 кг. В первые 10 сек. он проходит 35 м. Найти натяжение каната, на котором висит лифт.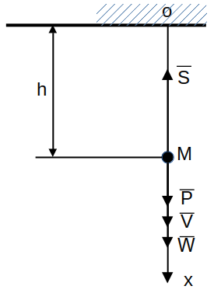

Дано:

h = 35 m \\ m = 280 kg.\\ t_1 = 10 c.\\ g=9.81 \frac{m}{c^2}

Определить:

\vert \overline S \vert = ?

Решение:

Направление оси \vec{ox} на рисунке выбираем совпадающим с направлением движения точки M, за которою принимаем рассматриваемое тело (лифт опускается).

Примечание: Рассматриваемое тело можно принимать за материальную точку, если оно совершает поступательное движение.

Запишем векторное уравнение динамики материальной точки

(1)   \begin{equation*} m \overline W = \sum^{n=2}_{j=1} \overline F_j \end{equation*}

в проекции на \overline{ox} уравнение (1) примет вид

(2)   \begin{equation*} m W_x = P_x+S_x, \end{equation*}

где сила тяжести точки

(3)   \begin{equation*} P_x=mg, \end{equation*}

сила натяжения троса

(4)   \begin{equation*} S_x = -S, \end{equation*}

(5)   \begin{equation*} W_x=W \end{equation*}

(так как движение точки прямолинейное, то W_y = W_z = 0)
Подставляя (3), (4), (5) в (2) получим

(6)   \begin{equation*} m W = mg - S \end{equation*}

Уравнение прямолинейного равноускоренного движения точки M имеет вид

(7)   \begin{equation*} x = x_0 + V_0 t + \frac{1}{2}W t^2 \end{equation*}

Подставляя x_0=0, V_0 = 0 (по умолчанию) в (7)

(8)   \begin{equation*} x = \frac{W t^2}{2} \end{equation*}

Подставляем в (8) t_1 = 10 c. и x=h = 35 m, получим

    \[ x = h = \frac{W t_1^2}{2}; \;\;\; W = \frac{2h}{t_1^2} = \frac{2 \times 35}{100} = 0.7 (\frac{m}{c^2}) \]

W — ускорение, с которым опускается точка M (лифт)

Из (6) \rightarrow S = mg - mW = mg ( 1 - \frac{W}{g}) = mg ( 1-N ); \;\;\; \frac{W}{g} = N — перегрузка;
Сделаем вычисления
S = 280 \times 9.81 \cdot ( 1 - \frac{0.7}{9.81} ) = 2550.8 H

Примечание: Обратим внимание, что перегрузка N = 0.7 / 9.81 = 0.0714 то есть много меньше единицы, а космонавты при полёте испытывают намного большие нагрузки, порядка 3, 4 единиц.

Ответ:

S = 2550.8 H \approx 2.55kH