Решить задачу (6.4) с учётом силы сопротивления воздуха движению, пропорциональной скорости тела. \overline R=-km\overline V, где m — масса тела, k — постоянный коэффициент (k>0).

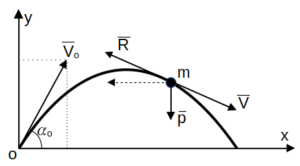
Дано:

R_x = -kmV_x
R_y = -kmV_y

Определить: y=f(x) — уравнение траектории точки


Запишем векторное уравнение динамики материальной точки

(1)   \begin{equation*} m \overline V = \overline p + \overline R \end{equation*}

(2)   \begin{equation*} mW_x = p_x+R_x \end{equation*}

p_x=0      ( \overline p \perp \vec ox ),      p_y=-mg      ( \overline p \parallel \vec oy и направлены противоположно )

(3)   \begin{equation*} mW_y = p_y+R_y \end{equation*}

(4)   \begin{equation*} W_x = \ddot x, W_y = \ddot y \end{equation*}

Подставим (4) в (2) и (3), получим

(5)   \begin{equation*} m \ddot x = - km\dot x \end{equation*}

(6)   \begin{equation*} m \ddot y = - km \dot y - mg \end{equation*}

Так как (m \neq 0), то сокращая на m, получим

(7)   \begin{equation*} \ddot x = -k \dot x \end{equation*}

(8)   \begin{equation*} \ddot y = -g -k \dot y \end{equation*}

Далее решаем по отдельности уравнения (7) и (8).

Для уравнения (7), которое теперь запишем в виде

    \[ \frac{d\dot x}{dt} = -k \dot x \]

Проинтегрируем, разделяя переменные \frac{d\dot x}{\dot x} = -kdt
\ln \dot x = -kt+C_1 (постоянную C_1 находим из начальных условий при t_0=0)
\ln V_0 \cdot \cos \alpha_0 = C_1

    \[ \ln \dot x = -kt + \ln \vert V_0 \cos \alpha_0 \vert \]

    \[ \ln \dot x - \ln \vert V_0 \cos \alpha_0 \vert = -kt \]

    \[ \ln \frac{\dot x}{V_0 \cdot \cos \alpha_0} = -kt \]

Потенцируем и получим

    \[ \frac{\dot x}{V_0 \cdot \cos \alpha_0} = e^{-kt} \]

(9)   \begin{equation*} \dot x = V_0 \cdot \cos \alpha_0 \cdot e^{-kt} \] \end{equation*}

Проинтегрируем второй раз, получим

    \[ \int dx = V_0 \cdot \cos \alpha_0 \int e^{-kt} \cdot dt \]

    \[ x = - \frac{V_0}{k} \cos \alpha_0 \cdot e^{-kt} + C_2 \]

(постоянную C_2 находим из начальных условий при t_0=0)

    \[ 0 = - \frac{V_0}{k} \cos \alpha_0 + C_2 \]

    \[ C_2 = \frac{V_0}{k} \cos \alpha_0 \]

    \[ x = - \frac{V_0}{k} \cos \alpha_0 \cdot e^{-kt} + \frac{V_0}{k} \cos \alpha_0 \]

(10)   \begin{equation*} x = - \frac{V_0}{k} \cos \alpha_0 ( 1 - e^{-kt} ) \] \end{equation*}

Для уравнения (8), которое теперь запишем в виде

    \[ \frac{d\dot y}{dt} = -k\dot y - g \]

Проинтегрируем

    \[ \int \frac{dy}{g+k\dot y} = - \int dt \]

(11)   \begin{equation*} \ln(g+k\dot y) = -kt+C_3 \end{equation*}

(постоянную C_3 находим из начальных условий при t_0=0)

    \[ \ln(g+kV_0 \sin \alpha_0}) = C_3 \]

Подставляя в (11) значение C_3, получим

    \[ \ln (g+k\dot y) = -kt + \ln(g+kV_0 \sin \alpha_0}), \]

тогда

    \[ \ln \frac{g+k\dot y}{g+kV_0 \sin \alpha_0}} = -kt \]

Потенцируем

    \[ \frac{g+k\dot y}{g+kV_0 \sin \alpha_0}} = e^{-kt} \]

С помощью алгебраических преобразований получим выражение для \dot y

    \[ g+k \dot y = ge^{-kt} + kV_0 \sin \alpha_0} \cdot e^{-kt} \]

(12)   \begin{equation*} \dot y = \frac{dy}{dt} = \frac{1}{k} (g + kV_0 \sin \alpha_0) e^{-kt} - \frac{g}{k} \end{equation*}

Интегрируем второй раз, получим

    \[ dy = \frac{1}{k} (g + kV_0 \sin \alpha_0) \cdot e^{-kt} \cdot dt - \frac{g}{k} \cdot dt \]

    \[ y = - \frac{1}{k^2} (g + kV_0 \sin \alpha_0) \cdot e^{-kt} - \frac{gt}{k} +C_4 \]

(постоянную C_4 находим из начальных условий при t_0=0)

    \[ 0 = - \frac{1}{k^2} (g + kV_0 \sin \alpha_0) - 0 + C_4\]

    \[ C_4 = \frac{1}{k^2} (g + kV_0 \sin \alpha_0) \]

Подставляем C_4 в уравнение (12), получим

    \[ y = - \frac{1}{k^2} (g + kV_0 \sin \alpha_0) e^{-kt} - \frac{g}{k}t + \frac{1}{k^2} (g + kV_0 \sin \alpha_0) \]

Получили y=f(t)

(13)   \begin{equation*} \[ y = \frac{1}{k^2} (g + kV_0 \sin \alpha_0)(1-e^{-kt})-\frac{g}{k}t \end{equation*}

Путём несложных преобразований, исключая из (10) и (13) параметр t, получим уравнение траектории точки в каноническом виде с учётом сопротивления движению:

(14)   \begin{equation*} y = \frac{1}{k} \frac{g + kV_0 \sin \alpha_0}{V_0 \cos \alpha_0} \cdot x - \frac{g}{k^2} ln(1-\frac{k \cdot x}{V_0 \cos \alpha_0}) \end{equation*}

Примечание:
В предыдущей задаче №3.1.2 мы получили решение в случае ОТСУТСТВИЯ сопротивления движению — траекторией является Парабола. Здесь уравнение (14) представляет так называемую «баллистическую кривую», но вид ее также не зависит от калибра (массы) снаряда, а только от угла бросания и начальной скорости V_0