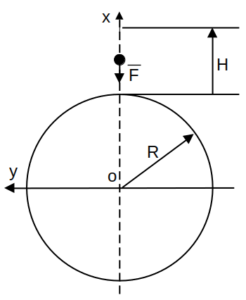
 Определить, какую направленную вверх наименьшую скорость
Определить, какую направленную вверх наименьшую скорость надо сообщить телу, чтобы оно поднялось на высоту H.
При подъёме считать силу притяжения изменяющейся обратно пропорционально квадрату расстояния от центра Земли. Сопротивлением воздуха пренебречь.
Дано:
Граничные условия:
при ,
тогда
,
— векторное уравнение движения точки,
в проекции на ось ox получим
,
, (умножаем обе части уравнения на dx), т.к.
интегрируем, получим
,
Ответ: