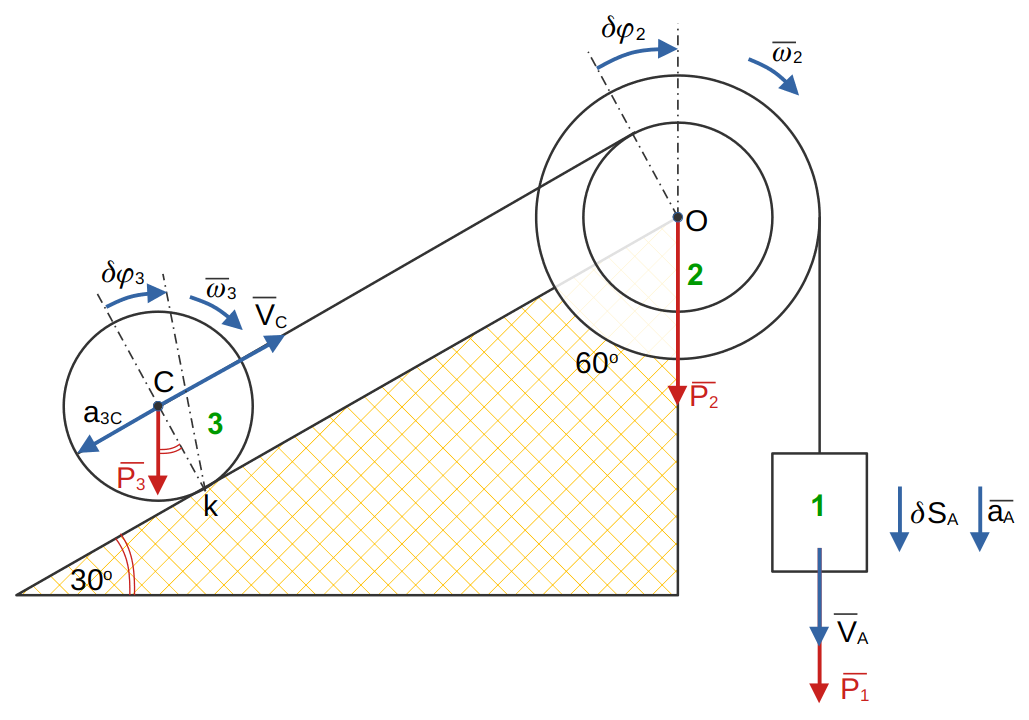
Нахождение ускорений тел механической системы (с одной степенью свободы) с помощью уравнений Лагранжа 2-го рода

Движение системы, которое начинается из состояния покоя, происходит под действием силы тяжести тела 1.
Массы тел 1,2,3, соответственно, равны m_1, m_2, m_3, ok 2 Блог 2-ступенчатый однородный цилиндр радиусов R_1, r_2 с моментом инерции относительно оси симметрии J.
Каток 3 — однородный цилиндр радиуса R_3.
Тела считать абсолютно твердыми а нити — абсолютно нерастяжимыми и невесомыми.
Найти ускорение центра тяжести тела 1 с помощью Общего Уравнения Динамики (ОУД), а также натяжение нитей.
Трением блока 2-3 о наклонную плоскость пренебречь.

Дано:

m_1, m_2, m_3, R_2, r_2, R_3,
J_2 = J
J_3_c = \frac{1}{2}m_3 R_3^2

Определить:

\overline a_1 = ?

Решение:

1. Возьмём за обобщённую координату S_A, тогда

V_A = \frac{dS_A}{dt} — обобщённая скорость

2. Определим кинетическую энергию системы в виде функции обобщённой скорости V_A:

(1)   \begin{equation*} T=T_1+T_2+T_3 \end{equation*}

Груз 1 совершает поступательное движение:

(2)   \begin{equation*} T_1 = \frac{m_1}{2} V_A^2 \end{equation*}

Ступенчатый цилиндр 2 вращается около неподвижной оси OZ:

(3)   \begin{equation*} T_2 = \frac{1}{2}J_2 \cdot \omega_2^2 \end{equation*}

Цилиндр 3 совершает плоско-параллельное движение (без проскальзывания):

(4)   \begin{equation*} T_3 = \frac{1}{2} m_3 V_C^2 + \frac{1}{2} J_{3C} \cdot \omega_3^2 \end{equation*}

Кинематические соотношения системы:

    \[ \omega_2 = \frac{V_A}{R_2} \]

    \[ \omega_3 = \frac{V_C}{R_3} \;\; : \;\; \frac{V_C}{V_A} = \frac{r_2}{R_2} \;\; \rightarrow \]

    \[ V_C = V_A \frac{r_2}{R_2} \]

    \[ \omega_3 = \frac{r_2}{R_3 \cdot R_2} \cdot V_A \]

3. Запишем (1) с учётом (2) — (4) и кинематических соотношений, получим,
обозначив T=\frac{1}{2}m^* \cdot V_A^2, (где m^* — приведённая масса системы)

(5)   \begin{equation*} \begin{split} T= \frac{m_1}{2}\cdot V_A^2 + \frac{J_2}{2R_2^2}\cdot V_A^2 + \frac{m_3}{2}\left(\frac{r_2}{R_2} \right)^2 \cdot V_A^2 = \\ = \frac{1}{2} \left[ m_1 + \frac{J_2}{2R_2^2} + \frac{m_3}{2}\left(\frac{r_2}{R_2} \right)^2 \right] V_A^2 \end{split} \end{equation*}

4. Составим уравнение Лагранжа 2-го рода:

(6)   \begin{equation*} \frac{d}{dt} \left( \frac{\partial T}{\partial V_A} \right) - \frac{\partial T}{\partial S_A} = Q \end{equation*}

    \[ m^* = \left[ m_1 + \frac{J_2}{2R_2^2} + \frac{m_3}{2} \left( \frac{r_2}{R_2} \right)^2 \right] \]

    \[ \frac{\partial T}{\partial S_A} = 0; \;\;\; \frac{\partial T}{\partial V_A} = m^*V_A; \]

    \[ \frac{d}{dt} \left[ \frac{\partial T}{\partial V_A} \right] = m^* \cdot \frac{dV_A}{dt} = m^* \cdot a_1, \;\;\;\left( a_1=\frac{dV_A}{dt} \right) \]

5. Определить обобщённую силу, соответствующую выбранной обобщённой координате S_A:

Запишем выражение для элементарной (виртуальной) работы сил, не зависящих от ограничений и сил сопротивления.

    \[ \delta A^e = m_1g \cdot \delta S_A - m_3 \sin 30^o \cdot g \delta S_{3C} = \]

подставим значения кинематических соотношений

    \[ \delta S_{3C} = \frac{r_2}{R_2} d S_A \]

а именно:

    \[ \begin{split} \delta A^e = m_1g \cdot dS_A - m_3g \cdot \sin 30^o \cdot \frac{r_2}{R_2} dS_A =\\ = g \left( m_1 - \frac{m_3 \cdot r_2}{2R_2} \right) \cdot dS_A \end{split} \]

Тогда, так как \delta A^e = Q \cdot dS_A, то
Q — обобщённая сила — правая часть уравнения (6)

5. Соединим левую и правую части уравнения (6):

m^* \cdot a_1 = Q, тогда a_1=\frac{Q}{m^*}

    \[ a_1 = a_A = \frac{ \left( m_1 - \frac{m_3}{2} \frac{r_2}{R_2} \right) g }{ m_1 + \frac{J_2}{R_2} + \frac{3}{2} m_3 \left( \frac{r_2}{R_2} \right)^2 } \]

— ускорение тела 1.

Примечание: Сравнить с решением задачи 13.1