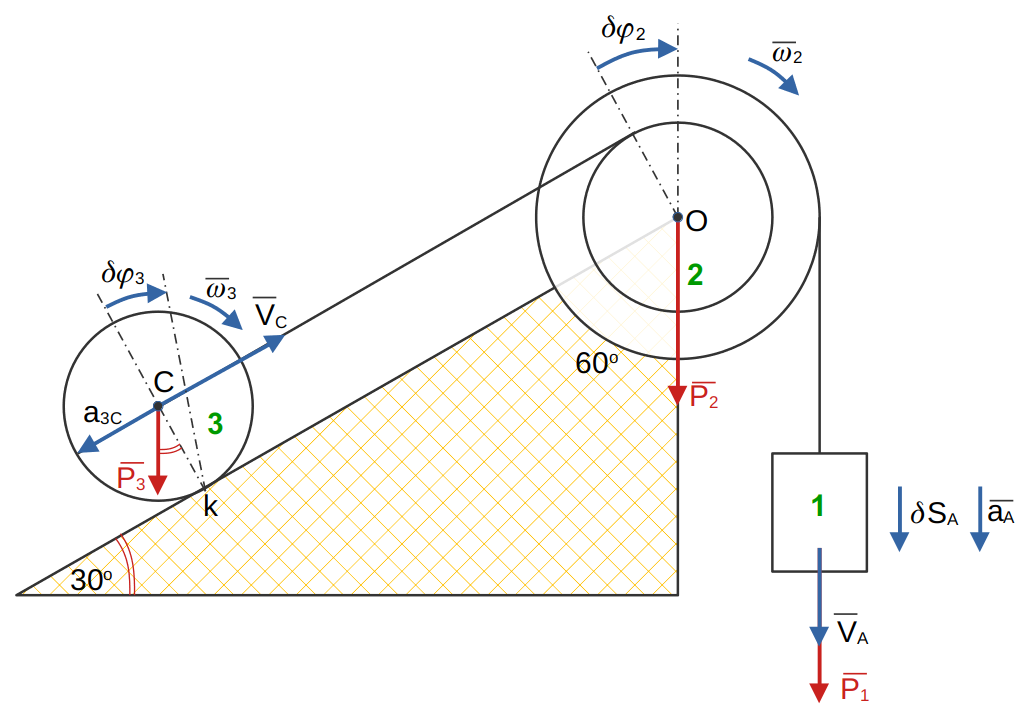
Движение системы, которое начинается из состояния покоя, происходит под действием силы тяжести тела 1.
Массы тел 1,2,3, соответственно, равны 2 Блог 2-ступенчатый однородный цилиндр радиусов
с моментом инерции относительно оси симметрии J.
Каток 3 — однородный цилиндр радиуса .
Тела считать абсолютно твердыми а нити — абсолютно нерастяжимыми и невесомыми.
Найти ускорение центра тяжести тела 1 с помощью Общего Уравнения Динамики (ОУД), а также натяжение нитей.
Трением блока 2-3 о наклонную плоскость пренебречь.
Дано:
Определить:
(ОУД)
(кинетостатика)
Решение:
I. Применим (ОУД) — общее уравнение динамики для опеределения: 
Изобразим ускорения точек и угловое ускорение звеньев (с условным направлением), так (см.рис.) и
,
соответственно, силы инерции и момент инерции добавим к активным силам системы (),
а именно: ,
и и момент
1. Запишем общее уравнение динамики (ОУД)
(1)
2. Сообщаем системе возможные элементарные перемещения и, составляя уравнение (1), получим
(при этом воспользуемся кинематическими соотношениями)
(2)
3. Выразим все возможные перемещения через , т.е.
4. Кинетические соотношения:
соотношения для уравнений
5. Подставим полученные кинематические соотношения в уравнение (2), получим:
(3)
Перепишем уравнение (3), при этом вынесем за фигурную скобку, тогда, чтобы уравнение (3) выполнялось, нужно выражение в фигурных скобках приравнять к нулю, т.к.
, получим
(4)
Решая уравнение (4) относительно , получим
(5)
— ускорение тела 1.
Примечание:
Движение тела 1 будет ускоренным при условии, что и замедленным если
II
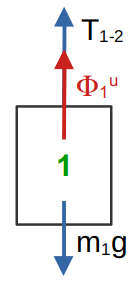 a). Определить натяжение нити на участке между телами 2 и 1: Применим принцип Д’Аламбера.
a). Определить натяжение нити на участке между телами 2 и 1: Применим принцип Д’Аламбера.
На рисунке
Сообщив телу 1 возможное перемещение и полагая условно, что тело 1 движется ускоренно под действием силы тяжести, и добавив силу инерции
, запишем в соответствии с принципом Д’Аламбера:
(6)
где -сила инерции, приложенная к телу 1.
— сила натяжения нити.
Из уравнения (6) получим: с учётом известного теперь из п.I значения для ускорения тела 1
Окончательно получаем:
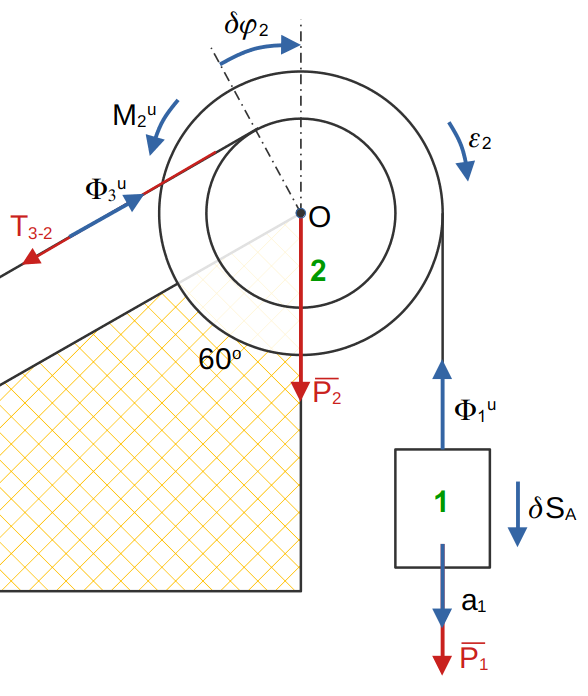
b). Определить натяжение нити на участке между телами 2 и 3.
Составим уравнение Д’Аламбера
(7)
С учётом кинематических соотношений перепишем (7) и получим
так как , то
(8)
Решая (8) относительно , получим ответ: