Задачи и решения | Татьянина математика в Раю теормеха

6.1 Решение прямой (первой) задачи динамики точки

26.1 [Мещерский И.В. Задачи по теоретической механике. // Изд-во. «Лань», 2008]

В шахте равноускоренно опускается лифт массой m=280 кг. В первые 10 сек. он проходит 35 м. Найти натяжение каната, на котором висит лифт.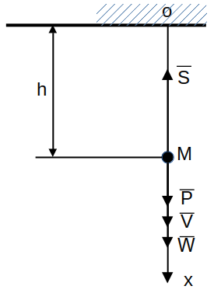

Читать далее→

14.1 Определение периода малых свободных колебаний и уравнения вынужденных малых колебаний (с одной степенью свободы)

Вариант №21 (из сборника Колебания механических систем: пособие по выполнению РГР / Г.Т. Алдошин, Н.Н. Дмитриев и др..; Балт. гос.техн. ун-т.-СПб., 2016.- 79 с.)

Однородное зубчатое колесо массой «m» и радиусом «r» находится во внешнем зацеплении с неподвижным колесом радиуса $R = 2r$ .

К оси подвижного колеса прикреплены две пружины (одинаковые), концы которых B и C расположены на горизонтальном диаметре неподвижного колеса. При $\varphi=0$ пружины находятся в свободном состоянии.

Пренебрегая весом кривошипа «ОА», определить:

Жёсткость пружины, при которой положение $\varphi=0$ является положением устойчивого равновесия.
Период малых свободных колебаний системы около данного положения равновесия
Малые колебания системы около положения равновесия $\varphi=0$ при нулевых начальных условиях если на кривошип действует момент $M_z = M_o e^{\frac{-\tau}{T}}$ , где $T$ — период свободных колебаний системы.

Читать далее→

15.1 Определение жесткости пружины из условия устойчивости положения равновесия системы сил, приложенных к механической системе, совершающей малые колебания (с одной степенью свободы)

Вариант №14 из сборника Колебания механических систем: пособие по выполнению РГР / Г.Т. Алдошин, Н.Н. Дмитриев и др..; Балт. гос.техн. ун-т.-СПб., 2016.- 79 с.)

Окружность радиусом R равномерно вращается с угловой скоростью $\omega$ вокруг вертикальной оси O.

По окружности может скользить без трения материальная точка M, имеющая массу m.

Определить:

Равновесные положения точки в ее движении относительно окружности;
Устойчивость этих положений;
Периоды свободных малых колебаний точки около устойчивых положений равновесия;
Малые вынужденные колебания точки около устойчивого положения равновесия $\varphi = 0$ , если ось вращения окружности O движется поступательно вдоль оси $\vec{ox}$ с постоянным ускорением w,а

Читать далее→

6.2 Решение обратной (второй) задачи динамики точки (прямолинейное движение)

Определить, какую направленную вверх наименьшую скорость $V_0$ надо сообщить телу, чтобы оно поднялось на высоту H.

При подъёме считать силу притяжения изменяющейся обратно пропорционально квадрату расстояния от центра Земли. Сопротивлением воздуха пренебречь.
Читать далее→

6.3 Решение обратной (второй) задачи динамики точки (криволинейное движение) в отсутствии силы сопротивления

Решить задачу (6.4) с учётом силы сопротивления воздуха движению, пропорциональной скорости тела. $\overline R=-km\overline V$ , где m — масса тела, k — постоянный коэффициент (k>0).

Дано:

$R_x = -kmV_x$
$R_y = -kmV_y$

Определить: y=f(x) — уравнение траектории точки

Читать далее→

2.1 Определение реакций связей при действии на тело ПРОСТРАНСТВЕННОЙ (произвольной) системы сил

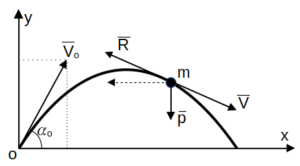
№ 8.24 (Из сб. И,В. Мещерский «Задачи по теоретической механике»/ «Лань», 2008.,448 с.)

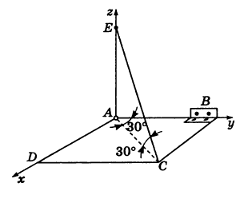Однородная прямоугольная рама веса 200 Н прикреплена к стене при помощи шарового шарнира A и петли B и удерживается в горизонтальном положении веревкой CE, привязанной в точке C рамы и к гвоздю E, вбитому в стену на одной вертикали с A, причем ∠ECA=∠BAC=30°. Определить натяжение веревки и опорные реакции.

Дано:

$P=200H$
$\alpha=30^o$

Определить:

$\overline R_A(X_A,Y_A,Z_A)$
$\overline R_B(X_B,0,Z_B)$
$\vert \overline T \vert = ?$

Читать далее→

2.2 Определение усилий в стержнях при действии пространственной системы сил

№ 8.28 (Из сб. И,В. Мещерский «Задачи по теоретической механике»/ «Лань», 2008.,448 с.)

Определить усилия в шести опорных стержнях, поддерживающих квадратную плиту ABCD, при действии горизонтальной силы P вдоль стороны AD. Размеры указаны на рисунке.

Дано:

$\overline P \parallel \overline{OY}$
$a$

Определить:

$S_i = ? \;\;\;\;\; (i=1..6)$

Читать далее→

2.3 Определение реакций связей для ворота при действии пространственной системы сил

$\overline F \parallel$ плоскости $A_{yz}$
$\overline S_1, \overline S_2 \parallel$ плоскости $A_{xy}$
$\overline T_1 \parallel T_2 \parallel$ плоскости $\overline{A_{xy}}$
$H_2 \cdot T_1 = T_2 = 2 \cdot 100 = 200H$
$S_1 = H_1 \cdot S_2 = 3 \cdot S_2;$

Дано:

$R = 0.5m$
$AB = 1.2m$
$G = 300H$
$T_1 = 100H$
$F = 100H$
$M = 10\cdot H_2 Hm$
$H_1 = 3.0$
$H_2 = 2.0$
$\alpha = 30^0$
$\beta = 60^0$
$\gamma = 30^0$
Читать далее→

6.4 Решение обратной (второй) задачи динамики точки (криволинейное движение) с учетом силы сопротивления

Тело брошено под углом $\alpha_o$ к горизонту со скоростью $\overline V_o$ . Определить уравнение траектории тела. Силами сопротивления пренебречь. Оси $\vec{ox}$ и $\vec{oy}$ изображены на рисунке.

Дано: $\alpha_o, \overline V_o$

Определить: $y=f(x)$

каноническое уравнение траектории
Читать далее→

Category Archives

Определить:

Дано:

Определить: y=f(x) — уравнение траектории точки

Дано:

Определить:

Дано:

Определить:

Дано:

Дано:

Определить:

Дано: $\alpha_o, \overline V_o$

Определить: $y=f(x)$