26.1 [Мещерский И.В. Задачи по теоретической механике. // Изд-во. «Лань», 2008]
В шахте равноускоренно опускается лифт массой m=280 кг. В первые 10 сек. он проходит 35 м. Найти натяжение каната, на котором висит лифт.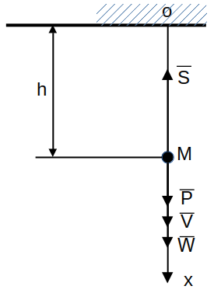
6.2 Решение обратной (второй) задачи динамики точки (прямолинейное движение)
Определить, какую направленную вверх наименьшую скорость 
надо сообщить телу, чтобы оно поднялось на высоту H.6.3 Решение обратной (второй) задачи динамики точки (криволинейное движение) в отсутствии силы сопротивления
Решить задачу (6.4) с учётом силы сопротивления воздуха движению, пропорциональной скорости тела. 
, где m — масса тела, k — постоянный коэффициент (k>0).
Дано:
к горизонту со скоростью 
. Определить уравнение траектории тела. Силами сопротивления пренебречь. Оси 
и 
изображены на рисунке.
