12. Уравнения Лагранжа 2-го рода | Татьянина математика в Раю теормеха

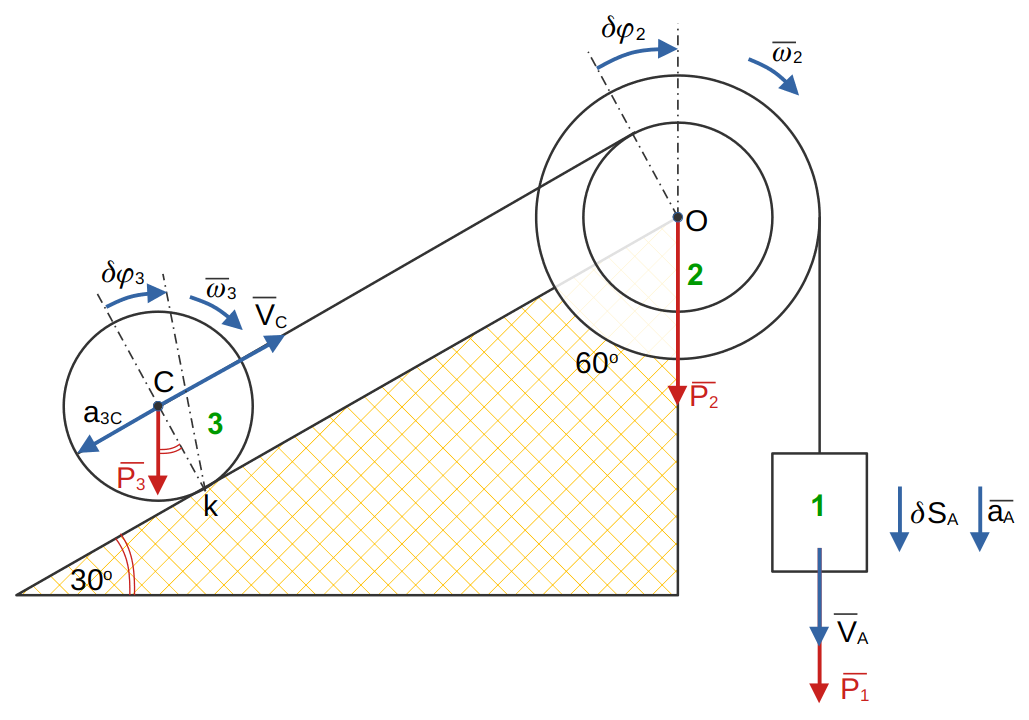
12.1 Нахождение ускорений тел механической системы (с одной степенью свободы) с помощью уравнений Лагранжа 2-го рода

Нахождение ускорений тел механической системы (с одной степенью свободы) с помощью уравнений Лагранжа 2-го рода

Движение системы, которое начинается из состояния покоя, происходит под действием силы тяжести тела 1.
Массы тел 1,2,3, соответственно, равны $m_1, m_2, m_3, ok$ 2 Блог 2-ступенчатый однородный цилиндр радиусов $R_1, r_2$ с моментом инерции относительно оси симметрии $J$ .
Каток 3 — однородный цилиндр радиуса $R_3$ .
Тела считать абсолютно твердыми а нити — абсолютно нерастяжимыми и невесомыми.
Найти ускорение центра тяжести тела 1 с помощью Общего Уравнения Динамики (ОУД), а также натяжение нитей.
Трением блока 2-3 о наклонную плоскость пренебречь.

Дано:

$m_1, m_2, m_3, R_2, r_2, R_3,$
$J_2 = J$
$J_3_c = \frac{1}{2}m_3 R_3^2$

Определить:

$\overline a_1 = ?$
Читать далее→

12.2 Нахождение ускорений тел механической системы (с двумя степенями свободы) с помощью уравнений Лагранжа 2-го рода

Однородная нить, к концу которой привязан груз А весом P, огибает неподвижный блок В, охватывает блок С, поднимается вверх на неподвижный блок D и проходит параллельно горизонтальной плоскости, где к ее концу привязан груз E веса P. Коэффициент трения скольжения груза E о горизонтальную плоскость равен f.
К оси блока С прикреплен груз К весом Q, под действием силы тяжести которого происходит движение системы.
Пренебрегая весом блоков В, С, D, определить ускорения грузов А, E, К и натяжение нити.