№ 23.57 (Из сб. И,В. Мещерский «Задачи по теоретической механике»/ «Лань», 2008.,448 с.)

Река Нева течет с востока на запад по параллели 60 градуса северной широты со скоростью V_r = 1.11 \frac{m}{c}
Найти составляющие абсолютного ускорения частицы воды.
Радиус Земли R = 64 \cdot 10^5m

Дано:

V_r = 1.11 \frac{m}{c}
\alpha = 60^o
R = 64 \cdot 10^5m — радиус Земной сферы

Определить:

\overline W_r, \overline W_e, \overline W_c = ?

Решение:

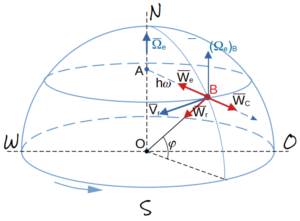
Переносное движение совершает сфера (Земля) — это вращение около оси ON с постоянной угловой скоростью \Omega_e
Относительное движение точки B по меридиану с севера на юг со скоростью V_r.
Результирующее (абсолютное) движение — со скоростью V_a.
Определим переносное ускорение точки B.
Запишем угловую скорость сферы (Земли) \Omega_e:

(1)   \begin{equation*} \Omega_e = \frac{2\pi}{24 \cdot 60 \cdot 60} = 7.29 \cdot 10^{-5} (c^{-1}) \end{equation*}

Относительное ускорение точки B:

(2)   \begin{equation*} \overline{W_r} = \overline W_{r\tau} + \overline W_{r\nu} \end{equation*}

W_{r\tau} = 0, т.к. V_r = const. (W_{r\tau} = \pm \vert \frac{dV_r}{dt}\vert ), тогда
\overline{W_r} = \overline W_{r\nu}

Нормальное относительное ускорение точки B равно:

(3)   \begin{equation*} W_{r\nu} = \frac{V_r^2}{R \cos \alpha} = \frac{1.11^2}{64 \cdot 10^5 \cdot 0.5} = 3.86 \cdot 10^{-7} (\frac{m}{c^2}) \end{equation*}

Переносное ускорение точки B равно:

(4)   \begin{equation*} \overline W_e = \overline W_{ej}^{oc} + \overline W_{er}^{bp} \end{equation*}

    \[ \vert \overline W_{r\nu}^{oc} \vert = \Omega_e^2 \cdot h\omega = (7.29 \cdot 10^{-5})^2 \cdot R \cos \varphi = \]

    \[ =(7.29 \cdot 10^{-5})^2 \cdot 64 \cdot 10^{-5} \cdot 0.5 = 1.700 \cdot 10^{-5} \frac{m}{c^2} \]

W_{er}^{bp} = 0, т.к. \xi_e = \frac{d Omega_e}{dt} = 0; \;\;\; (|omega_e = const).

(5)   \begin{equation*} W_e = 2 [ (\overline \Omega_e)_B \cdot x \overlive V_r ]; \end{equation*}

(\overline W_e \perp заштрихованной плоскости).

    \[ \vert \overline W_C \vert = 2 \vert \overline \Omega_e \vert \vert \overline V_r \vert \vert \underbrace{ \sin ( \overline \Omega^e , \overline V_r )}_{\sin 90^o = 1} \vert = \]

    \[ = 2 \cdot \Omega_e \cdot V_r = 2 \cdot 7.29 \cdot 10^{-5} \cdot 1.11 = 16.18 \cdot 10^{-5} (\frac{m}{c^2}) \]

    \[ \overline W_c = 2 [(\overline \omega_e)_m \cdot \overline V_r ]; \;\;\; \vert \overline W_c \vert = 2 \vert \overline \omega_e \vert \vert \overline V_r \vert \cdot \vert \sin ( \overline \omega_e, \overline V_r) \vert = 2\omega \cdot V_r \sin \alpha \]

Ответ: