№ 8.28  (Из сб. И,В. Мещерский «Задачи по теоретической механике»/ «Лань», 2008.,448 с.)

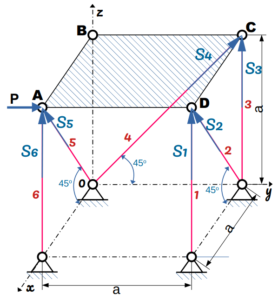
Определить усилия в шести опорных стержнях, поддерживающих квадратную плиту ABCD, при действии горизонтальной силы P вдоль стороны AD. Размеры указаны на рисунке.

Дано:

\overline P \parallel \overline{OY}
a

Определить:

S_i = ? \;\;\;\;\; (i=1..6)


Произвольная система сил F_j принадлежит \{ \overline P; \overline S_1,\overline S_2,\overline S_3,\overline S_4,\overline S_5,\overline S_6 \}

Примечание:
Векторы \overline S_2, \overline S_4 и \overline S_5 направлены по диагоналям квадратов, поэтому они наклонены под углом 45^o к его сторонам.

Запишем условия равновесия этой системы сил:

(1)   \begin{equation*} \sum_{j=1}^{n=7} F_{jx}=0; \;\;\; \vert\overline S_2 \vert \frac{\sqrt{2}}{2} + \vert\overline S_5 \vert \frac{\sqrt{2}}{2} = 0 \end{equation*}

(2)   \begin{equation*} \sum_{j=1}^{n=7} F_{jy}=0; \;\;\; \vert\overline S_4 \vert \frac{\sqrt{2}}{2} + \vert\overline P \vert = 0 \end{equation*}

(3)   \begin{equation*} \sum_{j=1}^{n=7} F_{jz}=0; \;\;\; \vert\overline S_1 \vert + \vert\overline S_2 \vert \frac{\sqrt{2}}{2} + \vert\overline S_3 \vert + \vert\overline S_4 \vert \frac{\sqrt{2}}{2} + \vert\overline S_5 \vert \frac{\sqrt{2}}{2} + + \vert\overline S_6 \vert = 0 \end{equation*}

(4)   \begin{equation*} \sum_{j=1}^{n=7} M_{ox}(\overline F_j)=0; \;\;\; \vert\overline S_1 \vert \cdot a + \vert\overline S_2 \vert \frac{\sqrt{2}}{2} \cdot a + \vert\overline S_3 \vert \cdot a = \vert \overline P \vert \cdot a = 0 \end{equation*}

(5)   \begin{equation*} \sum_{j=1}^{n=7} M_{oy}(\overline F_j)=0; \;\;\; -\vert\overline S_1 \vert \cdot a - \vert\overline S_6 \vert \cdot a = 0; \;\;\; \vert\overline S_1 \vert= - \vert\overline S_6 \vert \end{equation*}

(6)   \begin{equation*} \sum_{j=1}^{n=7} M_{oz}(\overline F_j)=0; \;\;\; -\vert\overline S_2 \vert \frac{\sqrt{2}}{2} \cdot a + \vert\overline P \vert \cdot a = 0; \end{equation*}

Решение:

Из (6) \rightarrow \vert\overline S_2 \vert = \frac{2 \vert\overline P \vert}{\sqrt{2}} = P \cdot \sqrt{2}

Из (1) \rightarrow \vert\overline S_5 \vert = - \vert\overline S_2 \vert = - P \cdot \sqrt{2}

Из (2) \rightarrow \vert\overline S_4 \vert = - P \cdot \sqrt{2}

Из (5) \rightarrow \vert\overline S_6 \vert = - \vert\overline S_1 \vert, тогда из (3) \rightarrow

    \[ \vert\overline S_1 \vert + ( \vert\overline S_2 \vert + \vert\overline S_4 \vert + \vert\overline S_5 \vert ) \frac{\sqrt{2}}{2} + \vert\overline S_3 \vert + \vert\overline S_6 \vert = 0 \]

    \[ \vert\overline S_3 \vert = - ( \vert\overline S_2 \vert + \vert\overline S_4 \vert + \vert\overline S_5 \vert ) \frac{\sqrt{2}}{2} = - ( P\sqrt{2} + P\sqrt{2} - P\sqrt{2} ) \frac{\sqrt{2}}{2} = \underline{-P} \]

Из (4) \rightarrow \vert\overline S_1 \vert = \vert\overline P \vert - \frac{\vert\overline S_2 \vert \sqrt{2}}{2} - \vert\overline S_3 \vert = P - P\sqrt{2} \cdot \frac{\sqrt{2}}{2} + P = \underline P;

Ответ:

S_1 = P, \;\;\;\; S_2 = P\cdot\sqrt{2}, \;\;\;\; S_3 = -P \;\;\;
S_4 = -P\cdot\sqrt{2}, \;\;\;\; S_5 = -P\cdot\sqrt{2}, \;\;\;\; S_6 = -P

Примечание 2:
Из решения уравнений (1) — (6) получили для модулей \vert S_4 \vert, \vert S_5 \vert и \vert S_6 \vert отрицательные значения, следовательно, надо условные направления векторов реакций стержней 4, 5, и 6 изменить на противоположные (на рис. указаны условные направления).
ВЫВОД : Стержни 1, 2 и 3 испытывают «РАСТЯЖЕНИЕ», а стержни 4,5 и 6 — «СЖАТИЕ»