Вариант №21 (из сборника Колебания механических систем: пособие по выполнению РГР / Г.Т. Алдошин, Н.Н. Дмитриев и др..; Балт. гос.техн. ун-т.-СПб., 2016.- 79 с.)
Однородное зубчатое колесо массой «m» и радиусом «r» находится во внешнем зацеплении с неподвижным колесом радиуса .
К оси подвижного колеса прикреплены две пружины (одинаковые), концы которых B и C расположены на горизонтальном диаметре неподвижного колеса. При пружины находятся в свободном состоянии.
Пренебрегая весом кривошипа «ОА», определить:
- Жёсткость пружины, при которой положение
является положением устойчивого равновесия.
- Период малых свободных колебаний системы около данного положения равновесия
- Малые колебания системы около положения равновесия
при нулевых начальных условиях если на кривошип действует момент
, где
— период свободных колебаний системы.
Дано:
Определить (1), (2), (3)
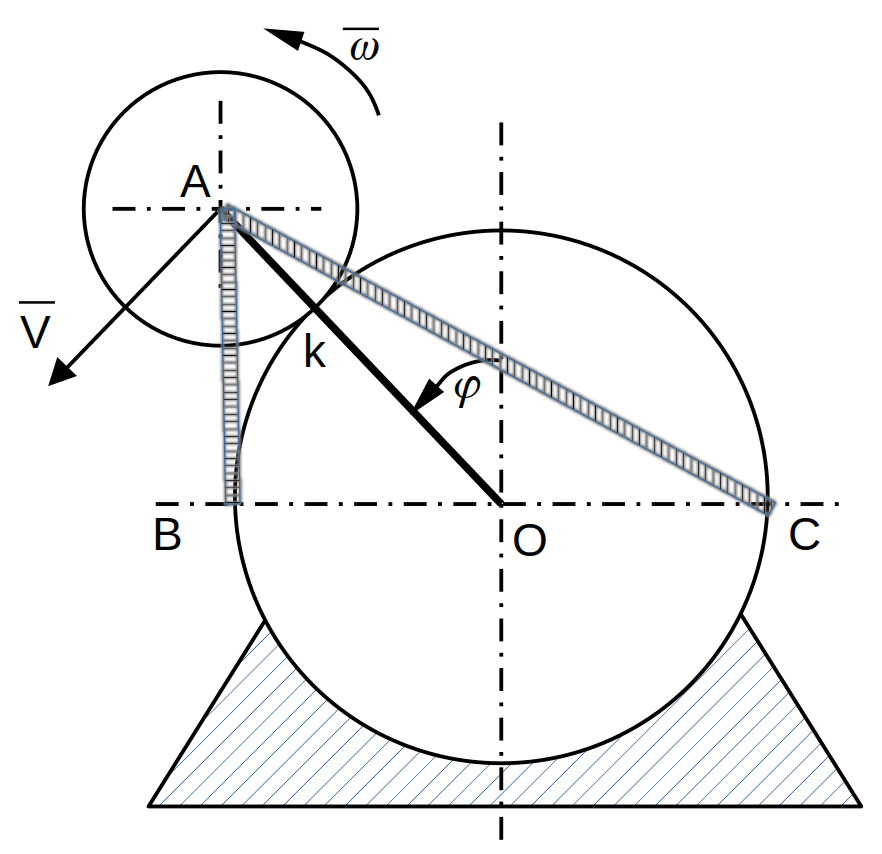
1. Определить жесткость пружины, при которой положение равновесия  является положением устойчивого равновесия.
является положением устойчивого равновесия.
Условие устойчивого положения равновесия:
(1),
(отсюда находится положение равновесия
).
За обобщенную координату принимаем ,
— обобщённая скорость.
Для нахождения потенциальной энергии системы:
константа.
(кстати, при
), т.е.
является положением равновесия системы.
; при
; получим
(
)
Примечание: Без пружин , неустойчиво.
Запишем выражение для потенциальной энергии системы, когда имеются пружины, жесткость которых следует определить, а именно:
при двух пружинах — (3).
(4).
(5), при
.
подставляем в (5) значение , получим:
, тогда
— жёсткость пружины, при которой
будет устойчиво.
2. Определить период малых колебаний системы около положения равновесия  …
…
(6), где k — циклическая частота малых свободных колебаний системы.
Дифференциальное уравнение свободных малых колебаний около положения равновесия:
(7) Однородное дифференциальное уравнение второго порядка с постоянными коэффициентами,
где (8)
— коэффициент квазиупругости (см. определение выше (5))
— коэффициент квазиинерционности.
— кинетическая энергия системы.
Подвижное колесо совершает плоско-параллельное движение, тогда
(9) , т.к.
, то
(10)
(11)
(12)
Подставляя (10) — (12) в (9), получим
, (13)
тогда (14)
С учётом (5) и (14) получим из (8) :
, тогда
(15)
— период малых свободных колебаний системы.
3. Записать уравнение малых колебаний системы при нулевых начальных условиях, если на кривошип действует момент  .
.
Дифференциальное уравнение вынужденных малых колебаний системы имеет вид:
(16)
(Для удобства записи обозначим )
Уравнение (16) — это неоднородное линейное дифференциальное уравнение с постоянными коэффициентами, решение уравнения (16) найдем в виде
(17), где
— Общее решение однородного уравнения (7)
— частное решение неоднородного уравнения (16), которое ищется в форме правой части уравнения (16).
(18)
k — циклическая частота (см.(8))
Пусть
(19)
Подставляем (19) в уравнение (16), получим
сравним коэффициенты при степени «e» в левой и правой части, получим, что
, отсюда
, тогда
(20)
вернёмся к (17), получим с учётом (18) и (20):
(21) — уравнение вынужденных колебаний системы
4. Определим произвольные постоянные  и
и  при нулевых начальных условиях :
при нулевых начальных условиях :  при
при 
Подставляя начальные условия в (21) получим:
см. (15)
(22)
, отсюда
(23)
Окончательно: подставим в (21) и (23), получим
— уравнение вынужденных малых колебаний при нулевых начальных условиях.