№ 23.47 (Из сб. И,В. Мещерский «Задачи по теоретической механике»/ «Лань», 2008.,448 с.)

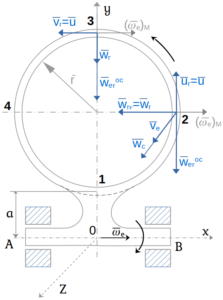Полое кольцо радиуса r жестко соединено с валом АВ, и притом так, что ось вала расположена в плоскости оси кольца. Кольцо заполнено жидкостью, движущейся в нем в направлении стрелки часов с постоянной относительной скоростью U.

Вал АВ вращается по направлению стрелки часов, если смотреть по оси вращения от А к В. Угловая скорость вала V постоянна.

Определить величины абсолютных ускорений частиц жидкости, расположенных в точках 1,2,3,4.

Дано:

U, \omega_o, r, a

Определить:

\overline W_{a,i} = ? \;\;\;\; (i=1,2,3,4)

Для i=2:

(1)   \begin{equation*} W_{a,r} = \overline W_r + \overline W_e + \overline W_c \end{equation*}

(2)   \begin{equation*} V_{a,r} = \overline V_r + \overline V_e \end{equation*}

\overline W_r — относительное ускорение точки M_2
\overline W_e — в переносном движении (вместе с кольцом).
\overline W_c — ускорение Кориолиса
Относительное движение точки M_2 — движение частиц жидкости по кольцу: \overline V_r = \overline U.
Переносное движение — вращение кольца вокруг оси AB:

(3)   \begin{equation*} V_e = \omega_e \cdot h_\omega = \omega_0 (r+a) \end{equation*}

h_\omega = (r+a), \;\;\;\;\;\; \overline \omega_e = \overline \omega_0 = \overline{const}

1. Рассмотрим относительное движение точки M_2:

(4)   \begin{equation*} \overline W_r = \overline W_{r\tau} + \overline W_{r\nu} \end{equation*}

\overline W_{r\tau} — касательное ускорение
\overline W_{r\nu} — нормальное (центростремительное) ускорение

(5)   \begin{equation*} W_{r\tau} = \frac{dV_r}{dt} = \frac{dU}{dt} = 0; \;\;\;\; (U = const) \end{equation*}

(6)   \begin{equation*} \overline W_r = \overline W_{r\nu}; \;\;\;\; \vert \overline W_{r\nu} \vert = \frac{V_r^2}{r} = \frac{U^2}{r} \end{equation*}

2. Рассмотрим переносное движение:

(7)   \begin{equation*} \overline W_e = \overline W_e^{bp} + \overline W_e^{oc} \end{equation*}

(8)   \begin{equation*} \vert \overline W_e^{bp} \vert = \varepsilon_e \cdot h_{\varepsilon_{M2}}, \;\;\;\;\; \varepsilon_e = \frac{d\omega_e}{dt} = \frac{d\omega_0}{dt} = 0; \;\;\; (\omega_0 = const) \end{equation*}

(9)   \begin{equation*} \overline W_e = \overline W_e^{oc}; \;\;\;\;\; \vert \overline W_e^{oc} \vert = \omega_e^2 \cdot h_{\omega_{M2}} = \omega_0^2 \cdot (a+r) \end{equation*}

3. Рассмотрим ускорение Кориолиса точки M_2:

(10)   \begin{equation*} \overline W_c = 2 [ ( \overline \omega_e )_M \cdot \overline V_r ] \end{equation*}

\overline W_c \uparrow\uparrow \vec{OZ} (см. рисунок)

(11)   \begin{equation*} \vert \overline W_c \vert = 2 \vert \overline \omega_e \vert \cdot \vert \overline V_r \vert \cdot \vert \underbrace{ \sin(\overline \omega_e, \overline V_r)}_{\sin 90^o=1} \vert = 2 \omega_0 \cdot U \end{equation*}

4. Определим абсолютное ускорение точки M_2

(используя метод сложения проекций):

Перепишем (1) с учётом (4), (7), (11), а также (5) и (8), получим

(12)   \begin{equation*} \overline W_{a,M_2} = \overline W_{r\tau} + \overline W_{r\nu} + \overline W_e^{oc} + \overline W_e^{bp} + \overline W_{c} = \overline W_{r\nu} + \overline W_e^{oc} + \overline W_c \end{equation*}

Проецируя (12) на оси координат \overline {OX} , \overline {OY} , \overline {OZ} и с учётом (6) и (9) и (11), получим

(13)   \begin{equation*} W_{ax} = W_{r\nu x} + W_{ex}^{oc} + W_{cx} = \frac{U^2}{r} \end{equation*}

(14)   \begin{equation*} W_{ay} = -W_{ey}^{oc} = -\omega_0^2 \cdot (a+r) \end{equation*}

(15)   \begin{equation*} W_{az} = W_c = 2 \cdot \omega_0 \cdot U \end{equation*}

Величина вектора абсолютного ускорения точки M2 по формулам сложения проекций определяется с учётом (13), (14), (15) :

    \[ \vert \overline W_{a,M_2} \vert = \sqrt{ W_{ax}^2 + W_{ay}^2 + W_{az}^2 } = \sqrt{ \frac{U^4}{r^2} + \omega_0^4 (a+r)^2 + 4 \omega_0^2 U^2 } \]

Для i=3:

Применяя по аналогии те же формулы (см. выше) получим

    \[ \overline W_{a,M_3} = \overline W_r + \overline W_e + \overline W_c \]

V_r = U \;\;\;\;\;\;\; (W_{r\tau}=0) (5)

А также (см. формулы (6) и (9) и (11) ):

\overline W_r = \overline W_{r\nu} ; \;\;\;\; W_{r\nu} = \frac{U^2}{r} ; \;\;\;\;\; \overline W_e = \overline W_{e}^{oc} :

    \[ W_e \arrowvert_{i=3} = \omega_e^2 \cdot h\omega_{M3} = \omega_e^2 (a+2r) = \omega_0^2 (a+2r) \]

    \[ \vert \overline W_c \vert = 2 \vert \overline \omega_e \vert \vert \overline U \vert \vert \underbrace{ \sin(\overline \omega_e, \overline V_r)}_{\sin 180^o=0} \vert = 0 \]

    \[ \vert \overline W_{a,M_3} \vert = \vert \overline W_r \vert + \vert \overline W_e \vert = \frac{U^2}{r} + \omega_0^2 (a+2r) \]

Для i=1:

…

Для i=4:

…