4.2.3 Определение угловых скоростей и ускорений звеньев и скоростей точек при плоско-параллельном (плоском) движении механизма (метод «Мгновенного центра скоростей» и метод » Полюса»)

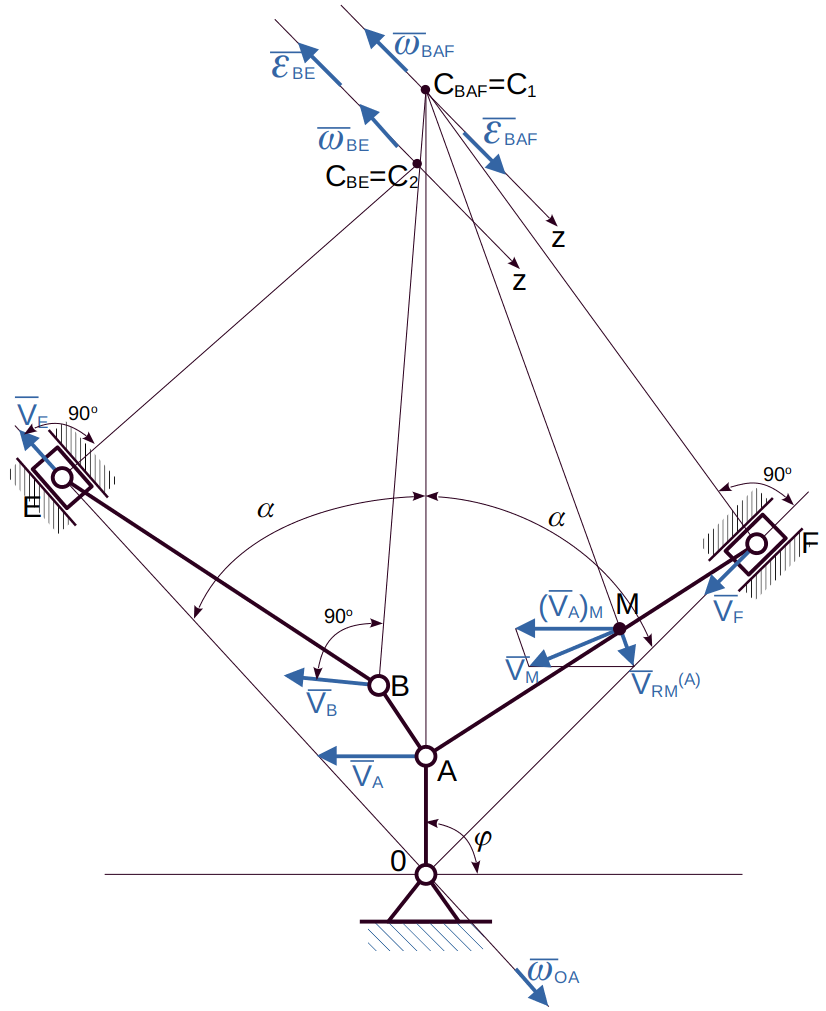
Рис.1

В положении механизма, указанном на рис.1, определить аналитически и построить на чертеже :

положение мгновенных центров скоростей всех звеньев, совершающих плоское движение;
скорости всех, точек механизма, расположенных в местах соединения звеньев (шарнирах);
угловые скорости всех звеньев;
ускорение точки А;
ускорений других точек механизма методом полюса;
угловые ускорения звеньев;
касательное и нормальное ускорения точки В;
установить характер движения точки В (ускоренное, замедленное, мгновенная остановка).

Дано:

$OA = 0.25m$
$AB = 0.20m$
$BE = 0.80m$
$AF = 0.85m$
$AM = 0.50m$
$\alpha = 45^o, \beta = 90^o$
$\varphi = 90^o$
$n_{OA}$ = 30 об./мин.

Определить:

1) $V_A, V_B, \overline V_F, \overline V_E$ = ?
2) $\overline \omega_{OA}, \overline \omega_{BAF}, \overline \omega_{BE}$ = ?
3) $\overline W_A, \overline W_B, \overline W_F, \overline W_E$ = ?
4) $\overline\varepsilon_{OA}, \overline\varepsilon_{BAF}, \overline\varepsilon_{BE}$ = ?

Решение:

I. Определим скорости точек и угловые скорости звеньев механизма (метод мгновенного центра скоростей, мцс)

1.1 Определим угловую скорость ведущего кривошипа OA:

$\omega_{OA} = \frac{2\pi n_{OA}}{60} = \frac{2\pi \cdot 30}{60} = \Pi (cek^{-1}) = 3.14 (cek^{-1})$

C1: вектор $\overline \omega_{OA} \in$ оси $\vec{OZ}$ — оси вращения кривошипа OA (см. рис.1), $\overline\omega_{OA} \uparrow\uparrow \vec_{OZ}$

1.2 Рассмотрим кривошип OA:

$V_A = \omega_{OA} \cdot \vert OA \vert = \Pi \cdot 0.25 \cong 0.78 (\frac{m}{c})$

C2: $\overline{V_A} \perp \overline{OA}$ в сторону вращения кривошипа OA (см. рис.1)

1.3 рассмотрим уголковый шатун BAF

Точка $C_{BAF} = C_1$ — мгновенный центр скоростей шатуна BAF
ось $\vec{C_1Z}$ — мгновенная ось вращения шатуна BAF.

(1) $\begin{equation*} \frac{V_F}{V_A} = \left|\frac{\vec C_1F}{\vec C_1A}\right| = \frac{1.21}{1.42} = 0.85; \end{equation*}$

Примечание: Так как на Рис.1 звенья механизма изображены в масштабе, то величины (размеры) мгновенных радиусов точек, а именно: $\vert C_1F \vert$ и $\vert C_1A \vert$ берутся с рисунка.

$V_F = V_A \cdot 0.85 = 0.78 \cdot 0.85 = 0.66 (m/c)$

C3: вектор скорости $\overline V_F \perp \overline{C_1F}$ по направляющей в сторону поворота шатуна (вниз).
Определим скорость точки B
Угловая скорость шатуна BAF:

(2) $\begin{equation*} \omega_{BAF} = \frac{V_A}{\vert \overline{C_1A} \vert } = \frac{0.78}{1.42} = 0.55 (cek^{-1}) \end{equation*}$

C4: Вектор $\overline \omega_{BAF} \uparrow\downarrow \overline{C_1Z}$ , т.к. шатун относительно оси $\vec{C_1Z}$ поворачивается по часовой стрелке.

(3) $\begin{equation*} \frac{V_B}{V_A} = \left| \frac{\vec C_1 B}{\vec C_1 A}\right| = \frac{1.30}{1.42} = 0.91 \end{equation*}$

Примечание: Величина $\vert C_1B \vert$ так-же берётся с Рис.1.
Из (3) получаем

$V_B = V_A \cdot 0.91 = 0.78 \cdot 0.91 = 0.71 (m/c)$

C5: вектор $\overline V_B \perp \overline{C_1 B}$ и направлен в сторону вращения шатуна BAF.

1.4 Рассмотрим шатун «BE»

Точка $C_2 = C_{BE}$ — мгновенный центр скоростей шатуна «BE»
Ось $\vec{C_2Z}$ — мгновенная ось вращения шатуна «BE»

(4) $\begin{equation*} \frac{V_E}{V_B} = \left|\frac{\vec C_2E}{\vec C_2B}\right| = \frac{1.01}{1.11} = 0.91; \end{equation*}$

Из (4) получаем:

$V_E = V_B \cdot 0.91 = 0.91 \cdot 0.71 = 0.65 (m/c)$

C6: Вектор $\overline{V_E} \perp \overline{C_2E}$ и направлен по направляющей вверх (см. Рис.1).
Угловая скорость шатуна BE:

(5) $\begin{equation*} \omega_{BE} = \frac{V_B}{\vert \vec C_2B \vert} = \frac{0.71}{1.11} = 0.64 (cek^{-1}) \end{equation*}$

Примечание: Величину $\vert \vec C_2B \vert$ берём из рис. 1 с учётом масштаба.

C7: вектор угловой скорости шатуна BE $\overline{\omega_{BE}} \uparrow\downarrow \vec{C_2Z}$ (от нас),
т.к. «отсюда» видим вращение по часовой стрелке относительно оси $\vec{C_2Z}$

1.5 Определим скорость точки M:

а) метод «мгновенного центра скоростей»:
Точка M $\in$ шатуну BAF, точка $C_1$ — мгновенный центр скоростей BAF, $C_1M$ — мгновенный радиус точки M.

(6) $\begin{equation*} \frac{V_M}{V_A} = \left|\frac{\vec C_1M}{\vec C_1A}\right| = \frac{1.23}{1.42} = 0.87 \end{equation*}$

Из (6) получаем:

$V_M = V_A \cdot 0.87 = 0.78 \cdot 0.87 = 0.68 (m/c)$

C8: Вектор скорости $\overline{V_M} \perp \vec{C_2M}$ и направлен в сторону вращения шатуна BAF
б) метод «полюса»: точка А — полюс

(7) $\begin{equation*} \overline V_M = \left( \overline V_A \right)_M + \overline V_{RM}^{(A)} \end{equation*}$

Где $\overline V_{RM}^{(A)}$ — вращательная скорость точки M относительно «полюса» A, вектор направлен перпендикулярно $\vec_{AM}$

$\overline V_{RM}^{(A)} = \left[ \overline \omega_{BAF} \cdot \vec{AM} \right] ;$

$\overline V_{RM}^{(A)} = \vert \overline \omega_{BAF} \vert \cdot \vert \vec{AM} \vert = 0.55 \cdot 0.5 = 0.28 (\frac{m}{c})$

$\vert \overline V_{M}^{(A)} \vert = \sqrt{ V_A^2 + (\overline V_{RM}^{(A)})^2 - 2 \vert \overline V_A \vert \cdot \vert \overline V_{RM}^{(A)} \vert \cdot \cos(\overline V_A;\overline V_{RM}^{(A)})} =$

$= \sqrt{ 0.78^2 + 0.28^2 - 2 \cdot 0.78 \cdot 0.28 \cdot 0.342 } = \sqrt{0.537} \cong 0.73(\frac{m}{c})$

$\cos 70^o$ = 0.342 (величина угла взята с рис.1)
Сравним $V_M$ = 0.68 m/c (мцс) и «метод полюса» $V_M$ = 0.73 m/c : погрешность расчёта составляет

$\Delta = \frac{0.73-0.68}{(0.73+0.68)/2} = \frac{0.05}{0.71} \cong 0.07 \;\;\; : \;\;\; \Delta = 7\% .$

II. Определение ускорений точек и угловых ускорений звеньев механизма. (методом «полюса»)

2.1 Ускорение точки A, принадлежащей кривошипу OA, который вращается вокруг неподвижной оси $\vec_{OZ}$

(8) $\begin{equation*} \overline W_A = \overline W_{RA}^{bp} + \overline W_{RA}^{oc} \end{equation*}$

(9) $\begin{equation*} \vert \overline W_{RA}^{bp} \vert = \vert \overline\varepsilon_{OA} \vert \cdot h_{\varepsilon A} = 0, \end{equation*}$

где $\overline W_{RA}^{bp}$ и $\overline W_{RA}^{oc}$ — вращательное и осестремительное ускорения точки A около оси $\vec_{OZ}$ соответственно.

(10) $\begin{equation*} \overline\varepsilon_{OA} = \frac{d\overline\omega_{OA}}{dt} = 0; \end{equation*}$

$(\omega_{OA}= const = \Pi c^{-1})$

С учётом (9) и (10) из (8) получим:

(11) $\begin{equation*} \overline W_{A} = \overline W_{BA}^{oc}; \end{equation*}$

(12) $\begin{equation*} \vert \overline W_{RA}^{oc} \vert = \omega_{OA}^2 \cdot \vert OA \vert = \Pi^2 \cdot 0.25 = 2.46 (\frac{m}{c^2}), \end{equation*}$

тогда их (11) с учётом (12) получим

$\vert \overline W_{A} \vert = 2.46 (\frac{m}{c^2})$

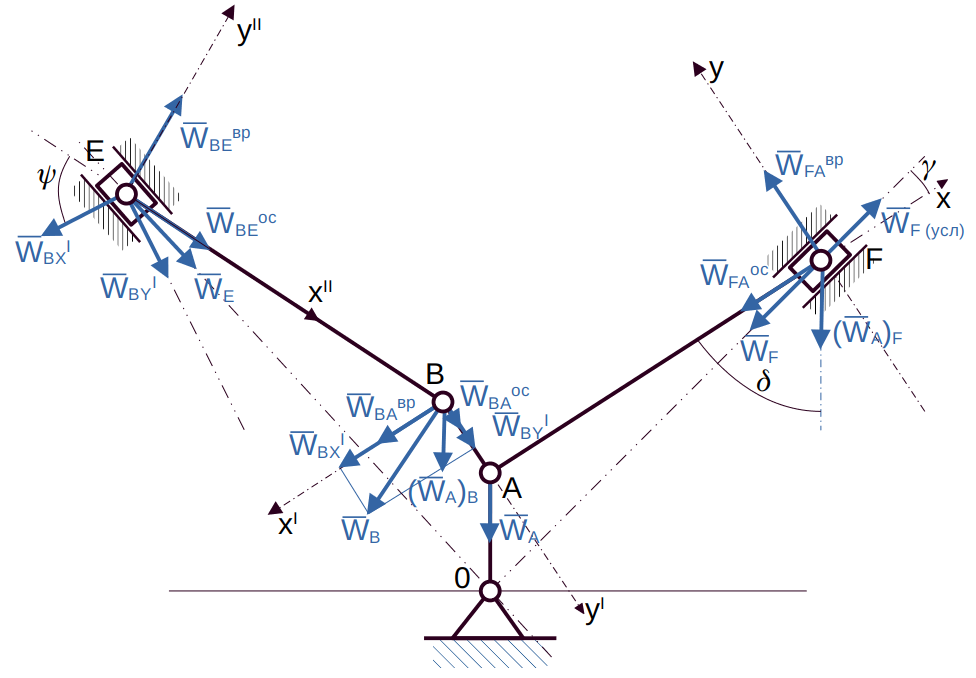
Рис.2

C9: $\overline{W_A}$ направлен из точки A к оси $\vec{OZ}$ (см.рис.2).

2.2 Рассмотрим шатун BAF

а) определяем ускорение точки F

(13) $\begin{equation*} \overline{W_F} = \left( \overline{W_A} \right)_F + \overline W_{FA}^{bp} + \overline W_{FA}^{oc}, \end{equation*}$

где $\overline W_{FA}^{bp}$ и $\overline W_{FA}^{oc}$ — вращательное и осестремительное ускорения точки F вокруг «полюса» A, соответственно.

(14) $\begin{equation*} \vert \overline W_{FA}^{oc} \vert = \omega_{BAF}^2 \cdot \vert \overline A F \vert = 0.55^2 \cdot 0.85 = 0.26 \frac{m}{c^2} \end{equation*}$

C10: Вектор осестремительного ускорения $\overline W_{FA}^{oc}$ направлен от точки F к «полюсу» A (см.рис.2)

C11: Для вектора вращательного ускорения $\overline W_{FA}^{bp}$ известна только линия действия (л.д.), $\overline W_{FA}^{bp} \perp \overline{AF}$ (направление также выбираем условно см.рис.2)

C12: Для вектора $\overline W_F$ — (ускорения «ползуна» F) известна только линия действия (л.д.) — направляющая «OF» (направление также выберем условно)

$\vert \overline W_{FA}^{bp} \vert = \vert \overline \varepsilon_{BAF} \vert \cdot \vert \overline{AF} \vert$

(15) $\begin{equation*} \varepsilon_{BAF} = \frac{ \vert \overline W_{FA}^{bp} \vert } { \vert \overline {AF} \vert } = ? \end{equation*}$

Спроектируем векторное равенство (13) на оси координат «XFY»:

на ось $\vec{FX}$ :

(16) $\begin{equation*} \vert\overline{W_F}\vert \cdot \cos \gamma = - \vert\overline{W_A}\vert \cdot \cos \delta - \vert \overline W_{FA}^{oc} \vert \end{equation*}$

на ось $\vec{FY}$ :

(17) $\begin{equation*} \vert W_F \vert \cdot \sin \gamma = - \vert\overline{W_A}\vert \cdot \sin \delta + \vert \overline W_{FA}^{bp} \vert \end{equation*}$

C13: $\gamma = 10^o; \;\;\; \delta = 55^o$ (см.рис.2)
$\sin\gamma = 0.17 \;\;\;\; \cos\gamma = 0.98$
$\sin\delta = 0.82 \;\;\;\; \cos\delta = 0.70$ , где величину этих углов берём с чертежа (см.рис.2)

Далее перепишем (16) и (17), подставляя числовые значения:

(18) $\begin{equation*} \vert\overline{W_F}\vert \cdot 0.98 = - \vert\overline{W_A}\vert \cdot 0.70 - 0.26 \end{equation*}$

(19) $\begin{equation*} \vert\overline{W_F}\vert \cdot 0.17 = - 2.46 \cdot 0.82 + \vert \overline W_{FA}^{bp} \vert \end{equation*}$

Из уравнения (16) получим:

$\vert\overline{W_F}\vert = - \frac{2.46 \cdot 0.70 + 0.26}{0.98} = - \frac{1.46}{0.98} = - 1.49 (\frac{m}{c^2}) < 0 \;\; !$

C14: Получили, что $\vert\overline{W_F}\vert < 0$ , следовательно, условное направление надо поменять на противоположное (см.рис.2)

Из уравнения (17) получим:

$\vert \overline W_{FA}^{bp} \vert = \vert\overline{W_F}\vert \cdot 0.17 + 2.46 \cdot 0.82 = 1.49 \cdot 0.17+2.02=2.27 (\frac{m}{c^2}) > 0$

C15: Так как $\vert \overline W_{FA}^{bp} \vert > 0$ , то условное направление верно! (см.рис.2).

Определим угловое ускорение шатуна BAF:

(20) $\begin{equation*} \vert \overline\varepsilon_{BAF} \vert = \frac{\vert \overline W_{FA}^{bp} \vert}{\vert \overline AF \vert} = \frac{2.27}{0.85} = 2.67 (cek^{-2}) \end{equation*}$

Направление $\overline\varepsilon_{BAF}$ определяем из векторного произведения
$\overline W_{FA}^{bp} = \left[ \overline\varepsilon_{BAF} \cdot \vec{AF} \right]$ (см.рис.2)

C16: Вектор $\overline W_{FA}^{bp} \uparrow\uparrow \vec{C_1Z}$ и, так как $\overline\varepsilon_{BAF} \uparrow\downarrow \overline\omega_{BAF}$ , то шатун «BAF» вращается замедленно ! (см.рис.1)

б) Определим ускорение точки $B \in BAF$ (метод «полюса»):

(21) $\begin{equation*} \overline W_B = \left(\overline W_A\right)_B + \overline W_{BA}^{bp} + \overline W_{BA}^{oc} \end{equation*}$

$\vert \overline W_{BA}^{oc} \vert = \omega_{BAF}^2 \cdot \vert \overline AB \vert = 0.55^2 \cdot 0.20 = 0.060 (\frac{m}{c^2})$

где $\omega_{BAF} = 0.55 c^{-1}$ (см. пункт I.)

C17: Вектор $\overline W_{BA}^{oc}$ направлен по $\overline{AB}$ от точки B к «полюсу» A (см.рис.2).
С учётом (20) получим, что:

$\vert \overline W_{BA}^{bp} \vert = \varepsilon_{BAF} \cdot \vert \overline{AB} \vert = 2.67 \cdot 0.20 = 0.53 (\frac{m}{c^2})$

(22) $\begin{equation*} \overline W_{BA}^{bp} = \left[ \overline\varepsilon_{BAF} \cdot \vert\vec{AB}\vert \right] \end{equation*}$

C18: Вектор $\overline W_{BA}^{bp} \perp \vec{AB}$ (см.рис.2).
Спроектируем векторное равенство (21) на оси $BXY$ :
на ось $\vec{BX}$

(23) $\begin{equation*} W_{BX} = \vert \overline W_A \vert \cdot \cos \lambda + \vert \overline W_{BA}^{bp} \vert \end{equation*}$

на ось $\vec{BY}$

(24) $\begin{equation*} W_{BY} = \vert \overline W_A \vert \cdot \sin \lambda + \vert \overline W_{BA}^{oc} \vert \end{equation*}$

$\lambda = 55^o, \;\;\; \sin \lambda = 0.82, \;\;\; \cos \lambda = 0.70$
угол $\lambda$ берём с чертежа (см.рис.2).
Перепишем (23) и (24), подставляя числовые значения:

(25) $\begin{equation*} W_{BX} = 2.46 \cdot 0.70 + 0.53 = 2.25 (\frac{m}{c^2}) \end{equation*}$

(26) $\begin{equation*} W_{BY} = 2.46 \cdot 0.82 + 0.060 = 2.08 (\frac{m}{c^2}) \end{equation*}$

Далее находим абсолютную величину ускорения точки B:

(27) $\begin{equation*} \vert \overline W_B \vert = \sqrt{ W_{BX}^2+W_{BY}^2 } = \sqrt{2.25^2+2.08^2} = \sqrt{5.06+4.33} = 3.06 (\frac{m}{c^2}) \end{equation*}$

Направление вектора $\overline W_B$ определяется направляющими косинусами по отношению к осям BXY.

(28) $\begin{equation*} \Bigg\{ \begin{matrix} \cos(\overline W_B^\wedge, \vec{BX}) = \frac{W_{BX}}{\vert \overline W_B \vert } = \frac{2.25}{3.06} = 0.74 \\ \cos(\overline W_B^\wedge, \vec{BY}) = \frac{W_{BY}}{\vert \overline W_B \vert } = \frac{2.08}{3.06} = 0.68 \end{matrix} \end{equation*}$

Соотношение (27) и (28) представляют вектор $\overline W_B$ по величине (27) и направлению (28)

2.3 Рассмотрим шатун «BE»

Запишем для $\overline W_E$ — вектора ускорения точки $E \in$ шатуну «BE» (по методу «полюса») векторное равенство:

(29) $\begin{equation*} \overline W_E = (\overline W_B)_E + \overline W_{BE}^{bp} + \overline W_{BE}^{oc} + (\overline W_{BX})_E + (\overline W_{BY})_E \end{equation*}$

Спроецируем (29) на оси координат $\vec Ex^{II}$ и $\vec Ey^{II}$ (см. рис.2)

(30) $\begin{equation*} \sin \psi \cdot \vert \overline W_E \vert = -\vert \overline W_{BX} \vert \cos \psi + \vert \overline W_{BY} \vert \sin\psi + \vert \overline W_{BE}^{oc} \vert \end{equation*}$

(31) $\begin{equation*} -\cos \psi \cdot \vert \overline W_E \vert = -\vert \overline W_{BX} \vert \sin \psi - \vert \overline W_{BY} \vert \cos\psi + \vert \overline W_{BE}^{bp} \vert \end{equation*}$

$\vert \overline W_{BE}^{oc} \vert = \omega_{BE}^2 \cdot \vert \overline{BE} \vert = 0.64^2 \cdot 0.80 = 0.33 (\frac{m}{c^2})$

Далее перепишем (30) и (31), подставляя числовые значения, получим

(32) $\begin{equation*} 0.259 \cdot \vert \overline W_E \vert = -2.25 \cdot 0.259 + 2.08 \cdot 0.80 + 0.33 \end{equation*}$

(33) $\begin{equation*} -0.966 \cdot \vert \overline W_E \vert = -2.25 \cdot 0.966 - 2.08 \cdot 0.259 + \vert \overline W_{BE}^{bp} \vert \end{equation*}$

Здесь также значение угла $\psi$ берём с чертежа (см.рис.2)

$\psi = 75^o; \;\;\;\; \cos\psi = 0.259; \;\;\;\; \sin\psi = 0.966$

Из (32) определим величину вектора ускорения точки E

$\vert \overline W_E \vert = \frac{1}{0.259} \left( -0.583 + 1.66 + 0.33 \right) = 4.50 (\frac{m}{c^2})$

Из (33) определим величину вектора вращательного ускорения точки «E» около «полюса» B:

$\vert \overline W_{BE}^{bp} \vert = -0.966 \cdot 4.50 + 2.25 \cdot 0.966 + 2.08 \cdot 0.259 =$

(34) $\begin{equation*} = -4.347 +2.17+0.538=-1.63 (\frac{m}{c^2}) \end{equation*}$

Определим величину углового ускорения шатуна BE с учётом (34)

$\vert \overline \varepsilon_{BE} \vert = \frac{\vert \overline W_{BE}^{bp} \vert}{\vert \overline{BE} \vert} = \frac{1.63}{0.80} = 2.04 (c^{-2})$

Направление вектора $\overline \varepsilon_{BE}$ определим из векторного произведения:

(35) $\begin{equation*} \overline W_{BE}^{bp} = \left[ \overline \varepsilon_{BE} \cdot \vec{BE} \right] \end{equation*}$

C19: Так как получили (34), что $\vert \overline W_{BE}^{bp} \vert < 0$ , то следует условное направление вектора изменить на противоположное (рис.2), тогда чтобы удовлетворить векторное произведение (35), вектор $\overline \varepsilon_{BE} \uparrow\downarrow \vec{C_2 Z}$ (см. рис.1), а поскольку получили, что $\overline \varepsilon_{BE} \uparrow\uparrow \overline \omega_{BE}$ , то, значит, характер вращения шатуна «BE» — ускоренный.

Ответ:

$\begin{matrix} V_A = 0.78 \frac{m}{c} & W_A = 2.46 \frac{m}{c^2} & \omega_{BAF} = 0.55 c^{-1} \\ V_B = 0.71 \frac{m}{c} & W_B = 3.06 \frac{m}{c^2} & \omega_{BE} = 0.64 c^{-1} \\ V_F = 0.66 \frac{m}{c} & W_F = 1.49 \frac{m}{c^2} & \varepsilon_{OA} = 0 \\ V_E = 0.65 \frac{m}{c} & W_E = 4.50 \frac{m}{c^2} & \varepsilon_{BAF} = 2.67 c^{-2} \\ V_M = 0.68 \frac{m}{c} & W_{OA} = 3.14 c^{-1} & \varepsilon_{BE} = 2.04 c^{-2} \end{matrix}$