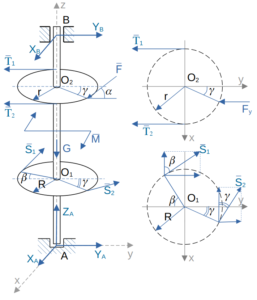
плоскости
плоскости
плоскости
Дано:
Определить:
Решение:
Система сил принадлежит
(1)
(2)
(3)
(4)
(5)
(6)
Из (6)
Из (5)
Из (4)
Из (3)
Из (2)
Из (1)
Ответ: