№ 8.24 (Из сб. И,В. Мещерский «Задачи по теоретической механике»/ «Лань», 2008.,448 с.)
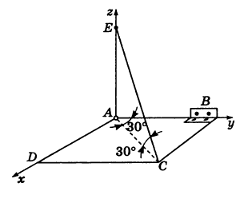 Однородная прямоугольная рама веса 200 Н прикреплена к стене при помощи шарового шарнира A и петли B и удерживается в горизонтальном положении веревкой CE, привязанной в точке C рамы и к гвоздю E, вбитому в стену на одной вертикали с A, причем ∠ECA=∠BAC=30°. Определить натяжение веревки и опорные реакции.
Однородная прямоугольная рама веса 200 Н прикреплена к стене при помощи шарового шарнира A и петли B и удерживается в горизонтальном положении веревкой CE, привязанной в точке C рамы и к гвоздю E, вбитому в стену на одной вертикали с A, причем ∠ECA=∠BAC=30°. Определить натяжение веревки и опорные реакции.
Дано:
Определить:
(1)
(2)
(3)
(4)
(5)
(6)
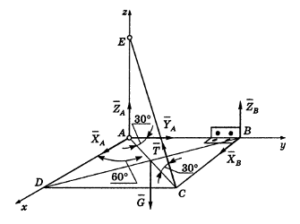
Из (6)
Из (5)
Из (4)
Из (3)
Из (2)
Из (1)
Ответ: