Вариант №14 из сборника Колебания механических систем: пособие по выполнению РГР / Г.Т. Алдошин, Н.Н. Дмитриев и др..; Балт. гос.техн. ун-т.-СПб., 2016.- 79 с.)
Окружность радиусом R равномерно вращается с угловой скоростью вокруг вертикальной оси O.
По окружности может скользить без трения материальная точка M, имеющая массу m.
Определить:
- Равновесные положения точки в ее движении относительно окружности;
- Устойчивость этих положений;
- Периоды свободных малых колебаний точки около устойчивых положений равновесия;
- Малые вынужденные колебания точки около устойчивого положения равновесия
, если ось вращения окружности O движется поступательно вдоль оси
с постоянным ускорением w,а
Решение
1. На точку действует сила сопротивления,  где
где  – скорость
– скорость
точки относительно окружности.
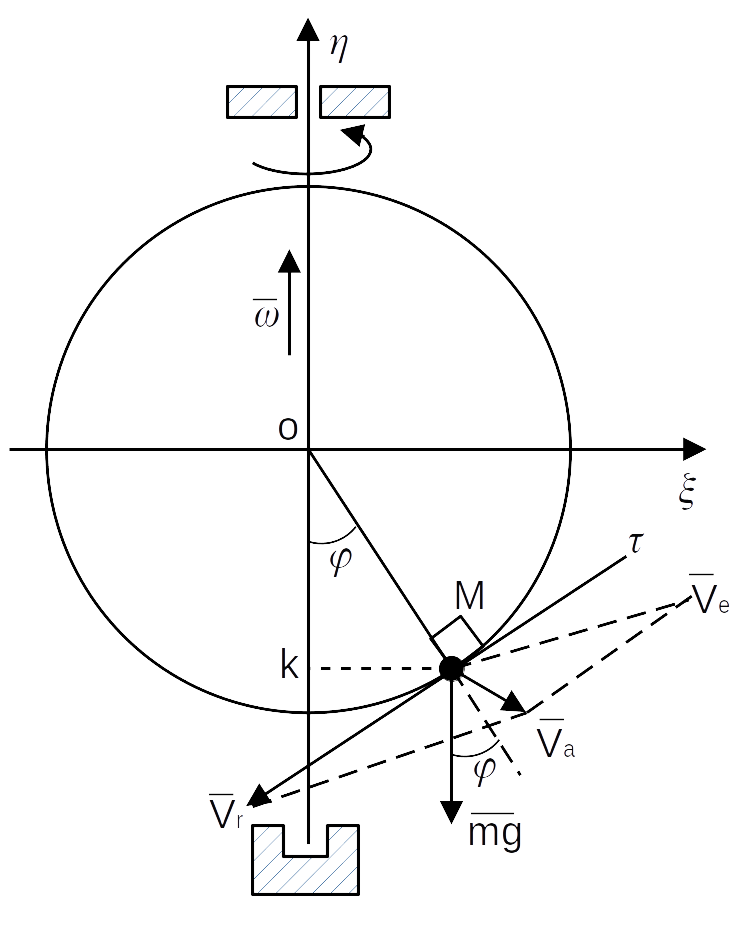
Примем за обобщённую координату , где
— обобщённая скорость. (Число степеней свободы равно 1)
2. Определим кинетическую энергию системы.
, но
, т.к. масса окружности мала по сравнения с массой точки M.
— абсолютная скорость точки М относительно неподвижной оси
, где
— переносная скорость точки М.
— плоскость окружности
— ,
принадлежит плоскости
(1)
— расстояние до оси
тогда ;
По теореме косинусов определим .
(2)
(3)
3. Подставляя (3) в выражение для кинетической энергии, получим
(4)
Используя (4), определим значение коэффициента квазиинерционности:
(5)
4.Теперь определим обобщенную силу Q, соответствующую выбранной обобщённой координате  и учитывая, что действующие силы на точку М консервативные, используем зависимость
и учитывая, что действующие силы на точку М консервативные, используем зависимость
(6)
обобщённую силу найдём из выражения для виртуальной работы
(7)
для случая с одной степенью свободы.
, то
(8)
Условие, из которого находим значение положения равновесия точки М:
(9)
, т.е.
5. Проверим устойчивость положений равновесия по критерию Лагранжа-Дирихле:
— положение равновесия устойчиво!
— положение равновесия неустойчиво!
: найдём вторую производную от потенциальной энергии точки М и подставим в полученное выражение значения
(10)
,
, устойчиво !!!
— неустойчиво!
Другой способ:
— потенциальная энергия.
;
( см. выше )
(см. выше, далее так же)
Коэффициент квазиупругости:
6. Определить период малых колебаний
(11)
— период малых свободных колебаний
при
подставляем a и c в формулу (11) получим
(12)
;
7. Рассмотрим вынужденные колебания точки М, если при этом на точку действует сила сопротивления.  и сама окружность перемещается вдоль оси
и сама окружность перемещается вдоль оси  с ускорением W=const.
с ускорением W=const.
(13)
(см. рис. 2)
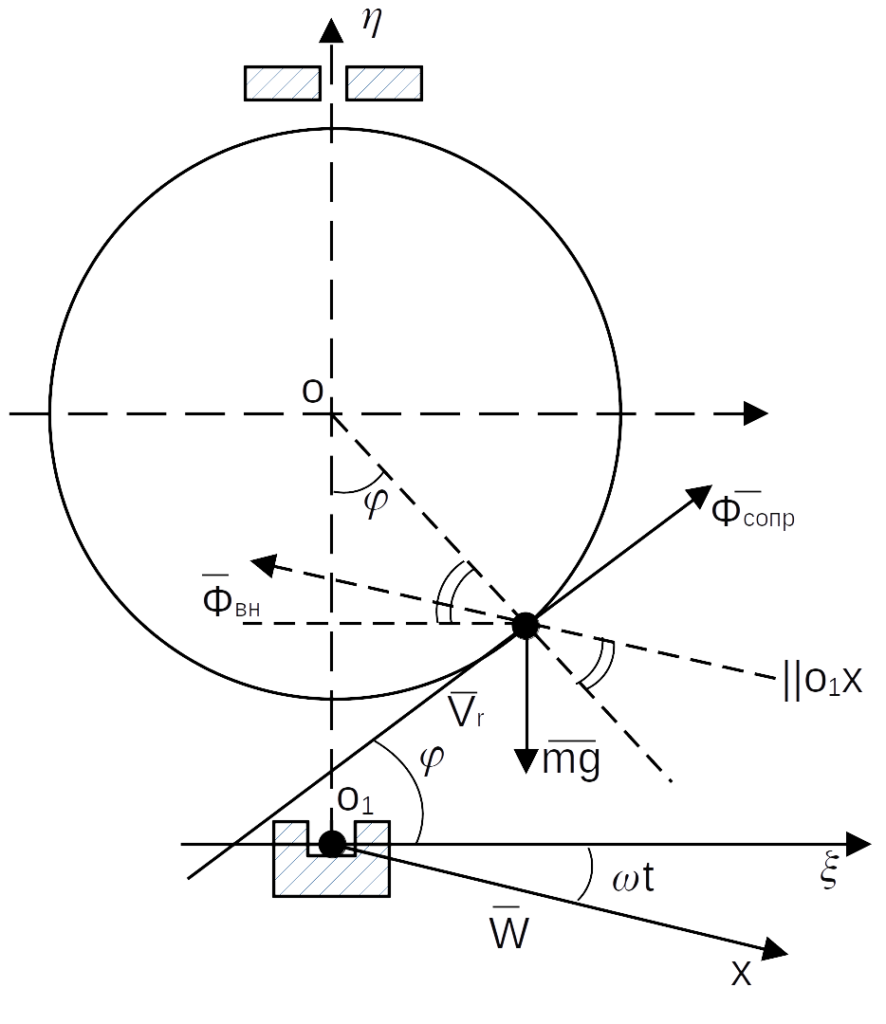
Запишем уравнение свободных малых колебаний в каноническом виде в присутствии силы сопротивления движению точки М.
(14)
с учётом вынуждающей силы уравнение вынужденных малых колебаний точки М около устойчивого положения равновесия (уравнение (14)) дополним:
(15)
8. Решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами (15):
Характеристическое уравнение имеет вид
(16)
( решаем однородное уравнение и найдём его общее решение, обозначим )
;
a) пусть , тогда
(17)
b) если , то
, (т.к.
)
(18)
в) если , то
(19)
Частное решение неоднородного уравнения (15) :
(20)
— подставляем в уравнение (15), получаем:
(21)
— полное решение уравнения.
сравним коэффициенты при одинаковых тригонометрических функциях:
, подставляем в (20), тогда
(22)
Вернёмся к уравнению (21), получим
а) ; уравнение вынужденных колебаний точки М если
б) ; уравнение вынужденных колебаний точки М если
в) — уравнение вынужденных колебаний точки М если