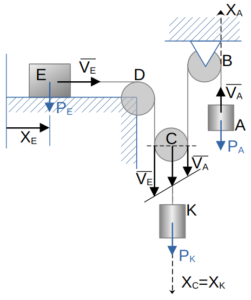
Однородная нить, к концу которой привязан груз А весом P, огибает неподвижный блок В, охватывает блок С, поднимается вверх на неподвижный блок D и проходит параллельно горизонтальной плоскости, где к ее концу привязан груз E веса P. Коэффициент трения скольжения груза E о горизонтальную плоскость равен f.
К оси блока С прикреплен груз К весом Q, под действием силы тяжести которого происходит движение системы.
Пренебрегая весом блоков В, С, D, определить ускорения грузов А, E, К и натяжение нити.

Дано:

P_A=P
P_E=P,f (коэффициент трения скольжения)
P_K=Q
P_B=P_C = P_D=0

Определить:

\overline W_A, \overline W_E, \overline W_K = ?
S_A = ? (натяжение нити)

Решение:
1) s=2, число степеней свободы:

q_1 = X_E, \;\;\; q_2=X_A :
\frac{dq_1}{dt} = \frac{dX_A}{dt} = V_A — обобщ. скорость
\frac{dq_2}{dt} = \frac{dX_E}{dt} = V_E — обобщ. скорость

2) Уравнения Лагранжа :

(1)   \begin{equation*} \frac{d}{dt} \left[ \frac{\partial T}{ \partial ( \frac{dX_A}{dt} )} \right] - \frac{\partial T}{\partial X_A} = Q_A \end{equation*}

(2)   \begin{equation*} \frac{d}{dt} \left[ \frac{\partial T}{ \partial ( \frac{dX_E}{dt} )} \right] - \frac{\partial T}{\partial X_E} = Q_E \end{equation*}

3) Определить кинетическую энергию системы:

T=T_A + T_E + T_K,
T_A = \frac{1}{2} \cdot \frac{P_A}{g} \cdot V_A^2 ; \;\;\;\; T_E = \frac{1}{2} \cdot \frac{P_E}{g} \cdot V_E^2 ; \;\;\;\; T_K = \frac{1}{2} \cdot \frac{P_K}{g} \cdot V_K^2 ;

Кинематические связи системы

(3)   \begin{equation*} V_C= \frac{V_A+V_E}{2} = \frac{1}{2} \left( \frac{dX_A}{dt} + \frac{dX_E}{dt} \right). \end{equation*}

Так как V_C=\frac{dX_C}{dt}, тогда \frac{dX_C}{dt} = \frac{1}{2} \left( \frac{dX_A}{dt} + \frac{dX_E}{dt} \right), отсюда после сокращения на dt получим элементарное перемещение груза C

(4)   \begin{equation*} dX_C = \frac{1}{2} \left( dX_A + dX_E \right), \end{equation*}

а так как при определении виртуальных перемещений ограничения становятся неизменяемыми, то

(5)   \begin{equation*} \delta X_C = \delta X_K = \frac{1}{2} \left( \delta X_A + \delta X_E \right), \end{equation*}

V_K=V_C (нить нерастяжимая)

Выразить кинетическую энергию системы через обобщённые скорости и координаты:

(6)   \begin{equation*} \begin{aligned} T = \frac{1}{2} \frac{P_A}{g} \left( \frac{dX_A}{dt} \right)^2 +\\ + \frac{1}{2} \frac{P_E}{g} \left( \frac{dX_E}{dt} \right)^2 +\\ + \frac{1}{2} \frac{P_K}{g} \left[ \frac{1}{2} \left( \frac{dX_A}{dt} +\\ + \frac{dX_E}{dt} \right) \right]^2 = \\ = \frac{1}{2} \frac{P_A}{g} \left( \frac{dX_A}{dt} \right)^2 +\\ + \frac{1}{2} \frac{P_E}{g} \left( \frac{dX_E}{dt} \right)^2 +\\ + \frac{1}{8} \frac{P_K}{g} \left[ \left( \frac{dX_A}{dt} \right)^2 +\\ + 2 \cdot \frac{dX_A}{dt} \cdot \frac{dX_E}{dt} +\\ + \left( \frac{dX_E}{dt} \right)^2 \right] = \\ = \frac{1}{8g} \cdot (4P+Q) \left( \frac{dX_A}{dt} \right)^2 +\\ + \frac{1}{8g} \cdot (4P+Q) \left( \frac{dX_E}{dt} \right)^2 +\\ + \frac{Q}{4g} \cdot \frac{dX_A}{dt} \cdot \frac{dX_E}{dt} ; \end{aligned} \end{equation*}

4) Определить обобщённые силы системы, соответствующие выбранным обобщённым координатам:

виртуальная работа приложенных к системе сил равна

(7)   \begin{equation*} \delta A = Q_A \cdot \delta X_A + Q_E \cdot \delta X_E ; \end{equation*}

Пользуясь тем, что обобщённые координаты не зависимы между собой, запишем отдельно а) и б), а именно:

a) \delta X_A \neq 0; \;\;\;\; \delta X_E = 0,
тогда \delta X_K = \frac{1}{2} \delta X_A (смотри (5) )

(8)   \begin{equation*} \delta A = \delta A_{P_A} + \delta A_{P_K} $ \end{equation*}

\delta A_{P_A} = - P_A \cdot \delta X_A;

(9)   \begin{equation*} \delta A_{P_K} = P_K \cdot \delta X_K; \end{equation*}

\delta A = \frac{1}{2}Q \cdot \delta X_A - P_A \cdot \delta X_A = \frac{1}{2} (Q-2P_A) \delta X_A

Q_A = \frac{1}{2}(Q-2P) — правая часть уравнения (1), множитель, стоящий в выражении для виртуальной работы перед вариацией обобщенной координаты, — обобщённая сила, соответствующая выбранной координате X_A.

б) \delta X_A = 0; \;\;\;\; \delta X_E \neq 0;
\delta A = \delta A_{P_K} + \delta A_{F_{mp}} — виртуальная работа с учётом трения скольжения
\delta A_{P_K} = P_K \cdot \delta X_K = Q \cdot \frac{1}{2} \delta X_E

(10)   \begin{equation*} \delta A_{F_{mp}} = -f \cdot P_E \cdot \delta X_E $ \end{equation*}

формулу (8) перепишем с учётом (10), получим

    \[ \delta A = \frac{1}{2} ( Q - 2fP_E ) \cdot \delta X_E = \frac{1}{2} ( Q - 2f P ) \cdot \delta X_E ; \]

Q_E = \frac{1}{2} ( Q - 2fP ) — правая часть уравнения (2) аналогично п. а) — обобщённая сила соответствующая выбранной координате X_E.

5) Составить уравнения Лагранжа (1) и (2)

для уравнения (1):

    \[ \frac{\partial T}{\partial X_A} = 0 ; \]

Взять частную производную по времени от кинетической энергии системы (6) по обобщённой скорости \frac{dX_A}{dt}

(11)   \begin{equation*} \left[ \frac{\partial T}{\partial \left( \frac{dX_A}{dt} \right) } \right] = \frac{4P+Q}{4g} \cdot \frac{dX_A}{dt} + \frac{Q}{4g} \cdot \frac{dX_E}{dt} \end{equation*}

Определить полную производную по времени от (11)

(12)   \begin{equation*} \frac{d}{dt} \left[ \frac{\partial T}{\partial \left( \frac{dX_A}{dt} \right) } \right] = \frac{4P+Q}{4g} \cdot \frac{d^2X_A}{dt^2} + \frac{Q}{4g} \cdot \frac{d^2X_E}{dt^2} : \end{equation*}

Перепишем (1) с учётом (11) и (12), получим

(13)   \begin{equation*} \frac{4P+Q}{4g} \cdot \frac{d^2X_A}{dt^2} + \frac{Q}{4g} \cdot \frac{d^2X_E}{dt^2} = \frac{1}{2} (Q - 2P ) \end{equation*}

перепишем уравнение (13) с учётом кинематических соотношений ( W_A=\frac{d^2X_A}{dt^2}, W_E=\frac{d^2X_E}{dt^2} ):

(14)   \begin{equation*} \frac{4P+Q}{4g} \cdot W_A + \frac{Q}{4g} \cdot W_E = \frac{1}{2} \cdot (Q-2P) \end{equation*}

для уравнения (2):

(15)   \begin{equation*} \frac{\partial T}{\partial X_E} = 0 ; \end{equation*}

Возьмем частную производную по времени от выражения для кинетической энергии (6) по обобщённой скорости \frac{dX_E}{dt}

(16)   \begin{equation*} \left[ \frac{\partial T}{\partial \left( \frac{dX_E}{dt} \right) } \right] = \frac{4P+Q}{4g} \cdot \frac{dX_E}{dt} + \frac{Q}{4g} \cdot \frac{dX_A}{dt} ; \end{equation*}

Полная производная по времени от (16) :

(17)   \begin{equation*} \frac{d}{dt} \left[ \frac{\partial T}{\partial \left( \frac{dX_E}{dt} \right) } \right] = \frac{4P+Q}{4g} \cdot \frac{d^2X_E}{dt^2} + \frac{Q}{4g} \cdot \frac{d^2X_A}{dt^2} ; \end{equation*}

Перепишем (2) с учётом кинематических соотношений (16) и (17), получим

(18)   \begin{equation*} \frac{4P+Q}{4g} \cdot \frac{d^2X_E}{dt^2} + \frac{Q}{4g} \cdot \frac{d^2X_A}{dt^2} = \frac{1}{2} (Q - 2fP ) \end{equation*}

перепишем уравнение (2):

    \[ \frac{4P+Q}{4g} \cdot W_E + \frac{Q}{4g} \cdot W_A = \frac{1}{2} \cdot (Q-2fP) \]

Решаем совместно алгебраические уравнения (13) и (18)

Обозначим:

    \begin{align*} a &= \frac{4P+Q}{4g}; & b &= \frac{Q}{4g} ; \\ c &= \frac{1}{2}(Q-2P); & d &= \frac{1}{2}(Q-2fP); \end{align*}

тогда уравнения перепишем с этими обозначениями, умножим каждое уравнение на b и a соответственно:

    \[ - \left\{ \begin{matrix} a \cdot W_A + b \cdot W_E = c \\ b \cdot W_A + a \cdot W_E = d \end{matrix} \qquad\qquad \bigg| \begin{matrix} \times b \\ \times a \end{matrix} \]

и вычтем почленно нижнее уравнение из верхнего

    \[ \left\{ \begin{matrix} a \cdot b \cdot W_A + b^2 \cdot W_E = c \cdot b \\ a \cdot b \cdot W_A + a^2 \cdot W_E = a \cdot d \end{matrix} \]

    \[ (b^2-a^2) \cdot W_E = (cb-ad) \]

(19)   \begin{equation*} \boldsymbol{W_E} = \frac{(cb-ad)}{(b^2-a^2)} \end{equation*}

подставляя (19) в верхнее уравнение системы, получим

    \[ ab \cdot W_A + \frac{b^2(cb-ad)}{(b^2-a^2)} = cb \]

    \[ \begin{split} W_A = \frac{cb}{ab} - \frac{b^2(cb-ad)}{ab (b^2-a^2)} = \\ = \frac{c}{a} - \frac{b}{a} \frac{(cb-ad)}{(b^2-a^2)} = \\ = \frac{1}{a} \bigg( \frac{c-cb^2+abd}{b^2-a^2} \bigg) = \\ = \frac{1}{a} \frac{cb^2-ca^2-cb^2-abd}{(b^2-a^2)} = \\ = \frac{-a(ca+bd)}{a(b^2-a^2)} = \frac{ac+bd}{a^2-b^2} \end{split} \]

т.е.: W_E = \frac{ad-cb}{a^2-b^2} (поменяем знаки в W_E).

    \[ \boldsymbol{W_K} = \frac{1}{2} (W_A+W_E) = \frac{1}{2} \frac{ac+bd+ad-cb}{(a^2-b^2)} = \frac{a(d+c)+b(d-c)}{(a^2-b^2)} \]

Обозначения: см. выше.

    \[ \boldsymbol{W_A} = \frac{ac+bd}{(a^2-b^2)} = \]

    \[ a^2-b^2 = \bigg(\frac{4P+Q}{4g}\bigg)^2 - \frac{Q^2}{16g} = \frac{16P^2+8PQ+Q^2-Q^2}{16g} = \frac{8P(2P+Q)}{16g} = \]

    \[ = \frac{P}{2g} \bigg(2P+Q\bigg). \]

    \[ ac+bd = \frac{4P+Q}{4g} \cdot \frac{1}{2} (Q-2P) + \frac{Q}{4g} \frac{1}{2} (Q-2Pf) = \]

    \[ = \frac{1}{8g} \Big[ 4PQ-8P^2+Q^2-2PQ+Q^2-PQf \Big] = \]

    \[ = \frac{1}{8g} \Big( 2Q^2+2PQ-8P^2-PQf \Big) \]

(20)   \begin{equation*} \begin{split} \boldsymbol{W_A} = \frac{1}{8g} \frac{(2Q^2+2PQ-8P^2-PQf) \cdot 2g}{P(2P+Q)} = \\ = \frac{(2Q^2+2PQ-8P^2-PQf)}{4P(2P+Q)}; \end{split} \end{equation*}

6) Определить натяжение нити S_a:

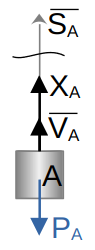Запишем уравнение динамики поступательного движения тела

    \[ \begin{matrix} m_A \cdot W_A = \vert \overline S_a \vert - P_A \\ \frac{P_A}{g} W_A = \vert \overline S_a \vert - P_A ; & ( P_A=P, & m_A=\frac{P_A}{g} ). \\ \vert \overline S_a \vert = \frac{P_A}{g} W_A + P_A ; \end{matrix} \]

подставляя в последнее уравнение значения W_A из (20) получим натяжение нити

    \[ \begin{split} \boldsymbol{\vert \overline S_a \vert} = \frac{P(2Q^2+2PQ-8P^2-PQf)}{4P(2P+Q)} + P = \\ = \frac{2Q^2+2PQ-8P^2-PQf+2P^2+PQ}{4(2P+Q)} = \\ = \frac{2Q^2+3PQ-6P^2-PQf}{4(2P+Q)} ; \end{split} \]

Примечание: Условное направление вектора \overline S_a выбрано верно, т.к. мы получили положительный ответ для модуля \vert\overline S_a\vert