Условие задачи:
Определить усилия в стержнях плоской фермы, находящейся под действием плоской системы сил.
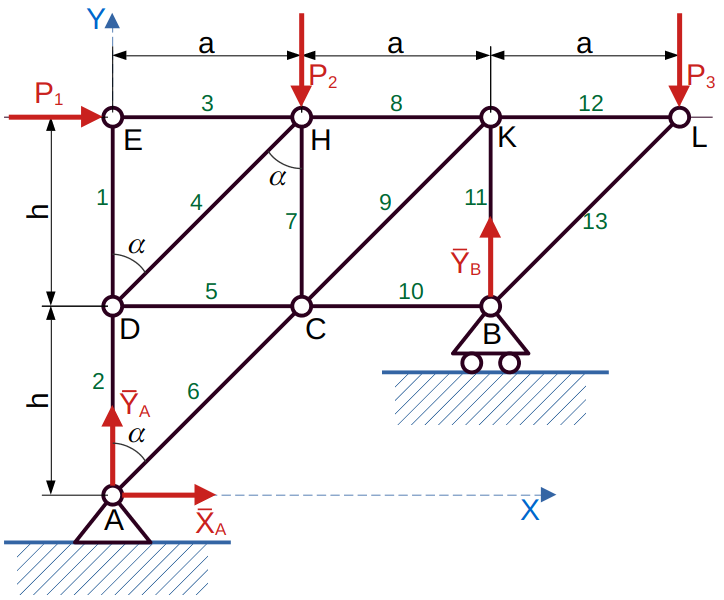
Рис.1
Дано:
(весом стержней пренебречь).
Определить:
Усилия в стержнях (методом вырезания узлов);
— (методом Риттера),
а так-же реакции опор .
Решение:
1. Определить реакции в опорах фермы.
(в точке A — неподвижный, а в точке B — подвижный шарниры)
Условия равновесия сил, приложенных к ферме :
(1)
(2)
(3)
Из (1) определим горизонтальную составляющую реакции в точке A:
Из (3) определим реакцию в точке B :
Из (2) определим вертикальную составляющую реакции в точке A:
Так как получили отрицательные значения для и
, то следует условные направления этих векторов изменить на противоположные (см. Рис.1)
2. Определение усилий в стержнях фермы (метод вырезания узлов)
Геометрия:
Вырезаем узлы.
Узел «A»
Условия равновесия сил, приложенных к узлу.
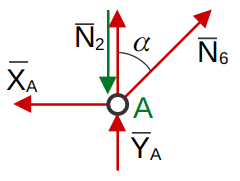
(4)
(5)
Из (4) определяем усилие в стержне 6:
Из (5) определяем с учётом полученного усилие в стержне 2:
Так как получили отрицательные значения для , то условное направление вектора (красная стрелка) следует изменить на противоположное (зелёная стрелка).
Узел «E»
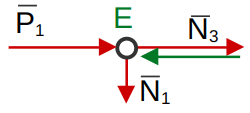
(6)
(7)
Узел «D»
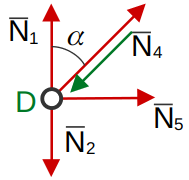
(8)
(9)
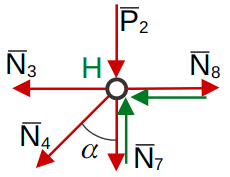
Узел «H»
(10)
(11)
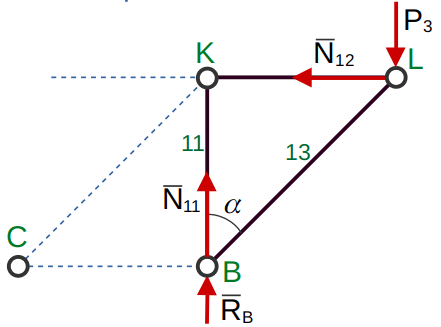
Узел «L»
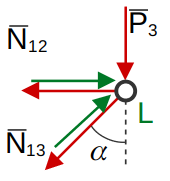
(12)
(13)
Узел «B»
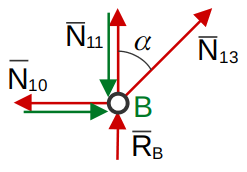
(14)
(15)
Узел «K»
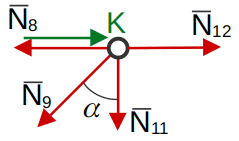
(16)
(17)
Узел «C»
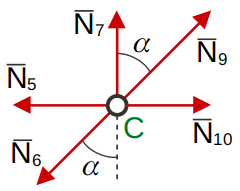
(18)
Проверка решения.
(19)
Так как условия (19) и (18) подтвердились, то проверка сходится.
Второй способ — определение усилий в стержнях  методом Риттера
методом Риттера
«Рассекаем» одним сечением два узла 8,9
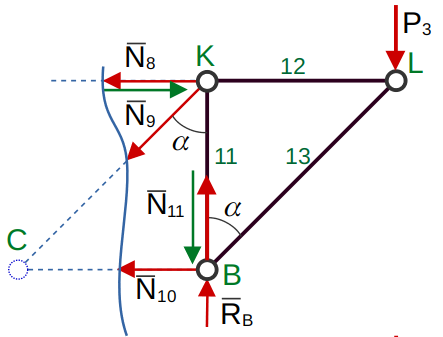
(20)
(21)
(22)
Сравнить полученные двумя способами (совпадение полное).
Результаты расчётов приведены в таблицах 1 и 2.
Таблица 1
| № стержня | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Усилие (kH) | 0 | 1 | 3 | 1.67 | 1.33 | 3.75 | 6 | 4.33 | 13.75 | 6.67 | 8.25 | 6.67 | 8.33 |
| «-» — сжатие «+» — растяжение |
‐ | ‐ | ‐ | + | + | ‐ | ‐ | + | ‐ | ‐ | + | ‐ |
Таблица 2
| 3.25 | 13.25 | -3 | -1.25 |
Ответ: