Тема: Равновесие сочленённых тел
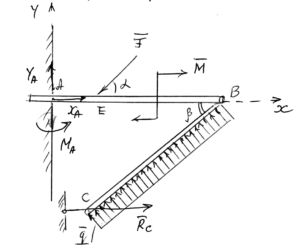 Дано:
Дано:
Определить:
Поскольку условий равновесия плоской системы всего ТРИ, а неизвестных в задаче БОЛЬШЕ, а именно ЧЕТЫРЕ, то следует применить метод «расчленения в промежуточном шарнире» (в точке В, см. Рис 1) и рассмотреть одну часть механизма (Рис. а), а действие «отброшенной» части (Рис. б) заменить реакцией в шарнире Rb (Xb,Yb) и рассмотреть отдельно равновесие этой части, в результате появляется ДВА дополнительных неизвестных (Xb,Yb), но число уравнений теперь — тоже ШЕСТЬ
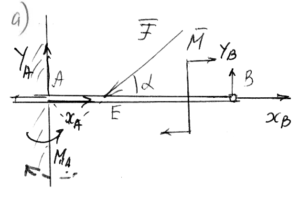 Рассмотрим (a):
Рассмотрим (a):
— система сил
и моментов
(1)
(2)
(3)
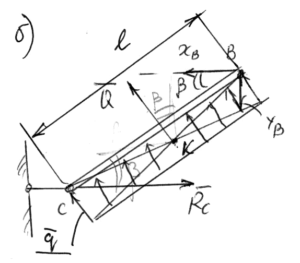 Рассмотрим (б):
Рассмотрим (б):
Величина результирующей силы распределенной нагрузки Q численно равна площади фигуры, по закону которой задано распределение, точкой приложения Q является ЦЕНТР тяжести этой фигуры (прямоугольника, точка пересечения диагоналей), направление результирующей силы Q совпадает с направлением стрелок распределенной нагрузки.
ДАЛЬШЕ см. формулу
(4)
(5)
(6)
Вычисления:
Из (6)
Из (5)
Из (4)
Из (2)
Комментарий: Так как , то условное направление вектора
следует изменить на противоположное!
Из (1)
Из (3)
Комментарий: Так как , то следует условное направление вектора
изменить на противоположное.
Ответ: