№ 4.28 (Из сб. И,В. Мещерский «Задачи по теоретической механике»/ «Лань», 2008.,448 с.)
Определить реакции заделки консольной балки, изображенной на рисунке и находящейся под действием равномерно распределенной нагрузки, сосредоточенной силы и пары сил.
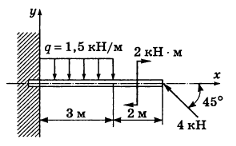 Дано:
Дано:
Определить:
Величина результирующей силы распределенной нагрузки Q численно равна площади фигуры, по закону которой задано распределение, точкой приложения Q является ЦЕНТР тяжести этой фигуры (прямоугольника, точка пересечения диагоналей), направление результирующей силы Q совпадает с направлением стрелок распределенной нагрузки.
ДАЛЬШЕ см. формулу
(1)
(2)
(3)
Из (3) =
=
=
Из (2)
Из (1)